この記事の動画解説版はこちら→統計チャンネル
$X$を,無数にある「9月のある1日」を選んだときの特定の都市における最高気温を表す確率変数とし,観測値$N=30$のとき,次のようなヒストグラムが得られたとする(記事02で扱ったもの).
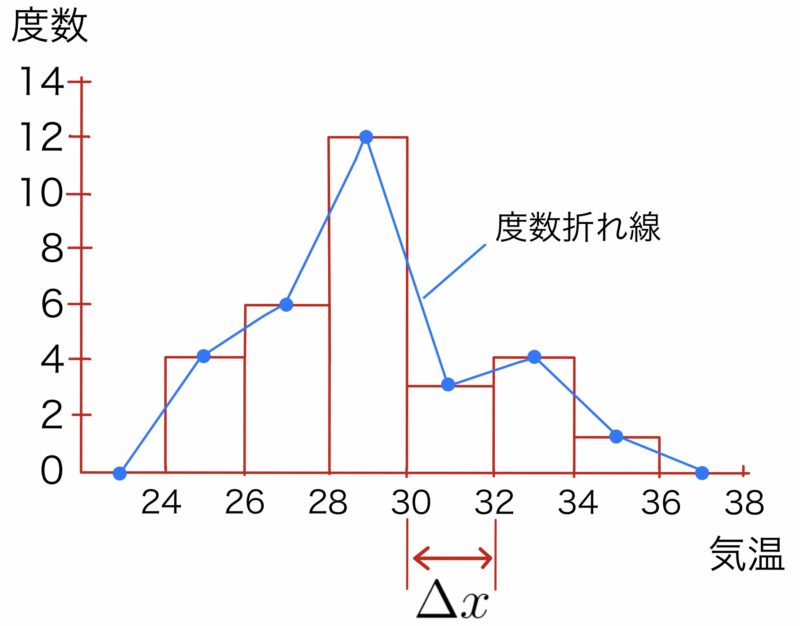
ヒストグラム の全面積$S$は
\( \displaystyle\begin{eqnarray} S &=&\sum (\mbox{各階級の度数})\times \Delta x\\ &=&\Delta x\sum (\mbox{各階級の度数})\\&=&2\times(4+6+12+3+4+1)=60 \end{eqnarray}\)
である.もとのヒストグラムについて,各柱の高さを$1/S$倍に縮めると全面積を$1$にすることができる.このとき,柱の面積はその階級の相対度数となる.例えば最高気温30℃以上32℃未満の日の割合は,対応する柱の面積$\frac{3}{60}\times 2=0.10 $により$10\%$となる.
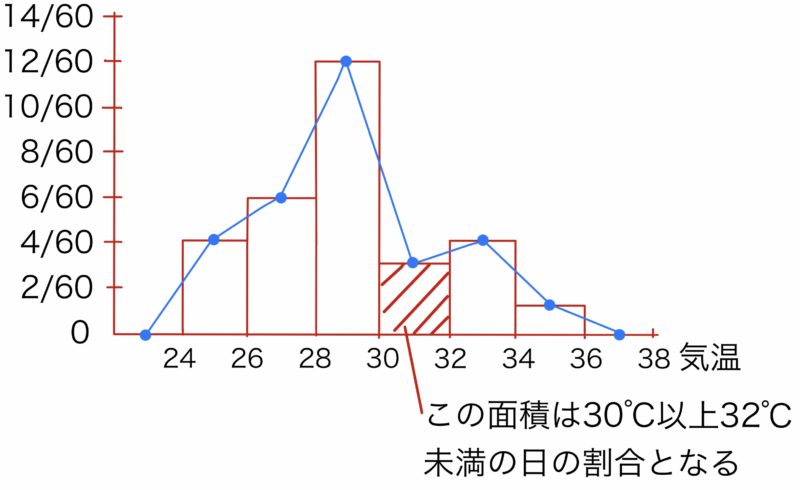
ここで,観測値を増やし,階級の幅を小さくする.すなわち$N\to\infty,\Delta x\to 0 $とすると,度数折れ線は次のようにある曲線$y=f(x)$に近づくと考えられる.$f(x)$を$X$の確率密度関数という.例えば,$X$が30℃以上32℃未満となる確率は積分で\( \displaystyle \int_{30}^{32}f(x)dx \)と表される(連続型確率変数においては,ある特定の1点をとる確率は0となるため,「32℃未満」を「32℃以下」に言い換えても同じ確率となる).
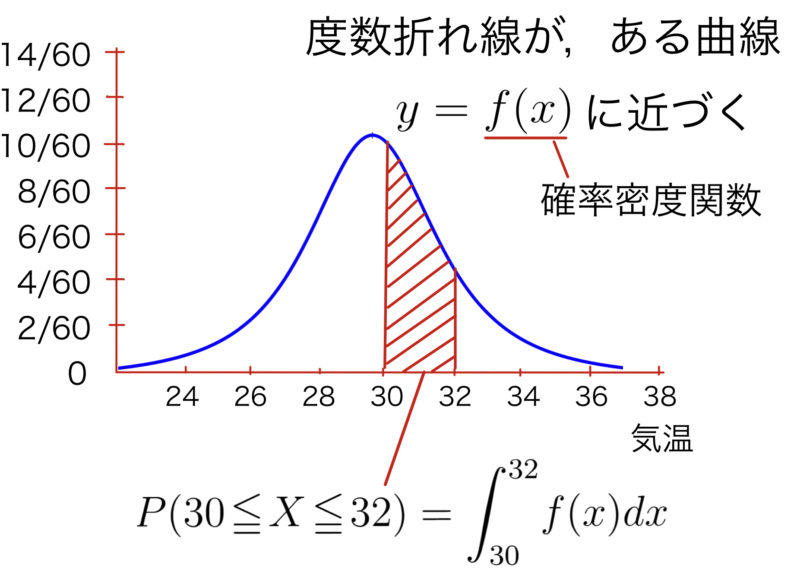
一般に,連続型の確率変数$X$は上のような確率密度関数(単に密度関数ともいう)$f(x)$をもつことが知られている.確率密度関数は次の(1)-(3)のような特徴がある.
\( \displaystyle\begin{eqnarray} (1)&&\displaystyle f(x)\geqq 0\\ (2)&&\int_{-\infty}^{\infty}f(x)dx=1 \\(3)&&P(a\leqq X\leqq b)=\int_{a}^{b}f(x)dx \end{eqnarray}\)
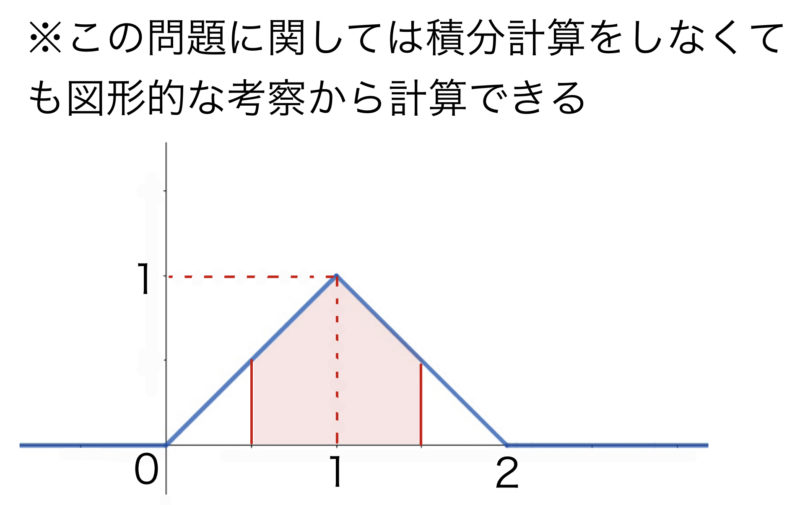
確率変数$X$の密度関数$f(x)$が次のように与えられている.
$f(x)=\begin{cases}
ax\ &(0\leqq x\leqq 1) \\
a(2-x)\ &(1\leqq x\leqq 2)\\
0 &(\mbox{それ以外})
\end{cases}$
(1) 定数$a$の値を求めよ.
(2) $P(0.5\leqq X\leqq 1.5)$を求めよ.
この記事の動画解説版はこちら↓
| 前の記事へ戻る 25 幾何分布 |
次の記事へ 27 連続型確率変数の平均や分散 |
| 記事一覧へ戻る 統計学の基礎シリーズ 目次 |
|