この記事の動画解説版はこちら→統計チャンネル
量的変数の観測値の整理のために,度数分布表やヒストグラムが使われる.例として,次のデータを度数分布表やヒストグラムにまとめてみよう.
(例)ある都市における9月の最高気温の観測値(℃)
35.8 33.3 33.7 30.5 29.1 28.0 29.2 28.9 28.4 27.9
27.3 31.5 32.5 32.0 29.3 29.4 28.7 28.7 28.9 29.2
29.8 30.3 27.1 26.4 24.5 24.3 24.2 25.3 26.2 26.8
量的変数を度数分布表にまとめる際には,ある程度の幅をもたせた区間,すなわち階級を設定する.この階級の設定の仕方はある程度目安になる公式があるが,最終的にはデータの様子をみて適切に設定する.今回の例ではスタージェスの公式(後で紹介する)から階級の数は6程度が目安で,最高気温35.8℃,最低気温が24.2℃であることから,24℃から2℃刻みで6つの階級を設定することとする.階級値は階級の幅のちょうど真ん中の値のこと,度数はその階級に含まれる観測値の個数である.先ほどの例の観測値をまとめると次のようになる.
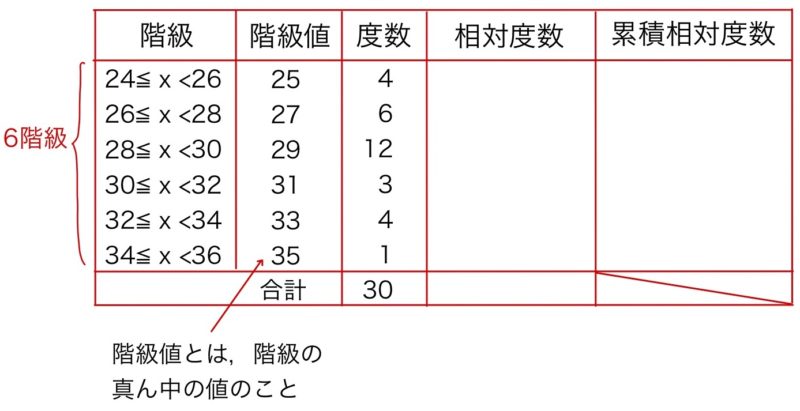
相対度数はその度数の観測値全体に占める割合,累積相対度数はその階級以前の度数の観測値全体に占める割合である.この例の図では階級値,相対度数,累積相対度数をすべて表にまとめているが,常に全部を表にする必要はなく,必要に応じた形でまとめればよい.
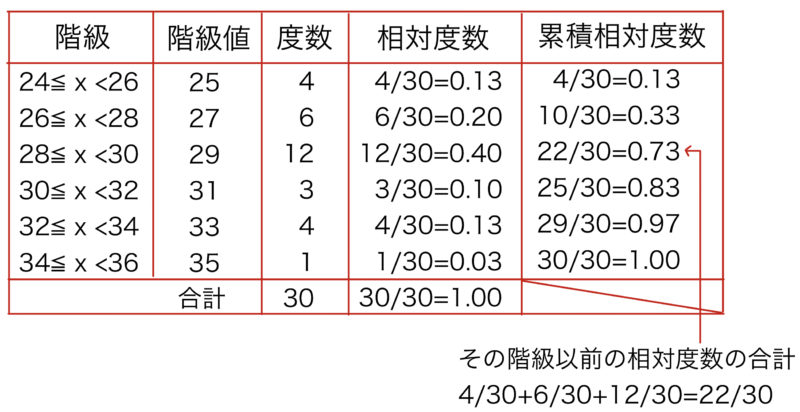
上の度数分布表をもとにヒストグラムを作成すると,次のようになる.この図にはヒストグラムに度数折れ線と呼ばれる線も追加して書いている.度数折れ線はヒストグラムの各柱の上底の中点を結んでできるグラフである(観測値を大きくし,階級の幅を狭くするとなるとなめらかな曲線になっていく.これが連続型確率変数の確率密度関数の考えにつながる.記事26を参照).
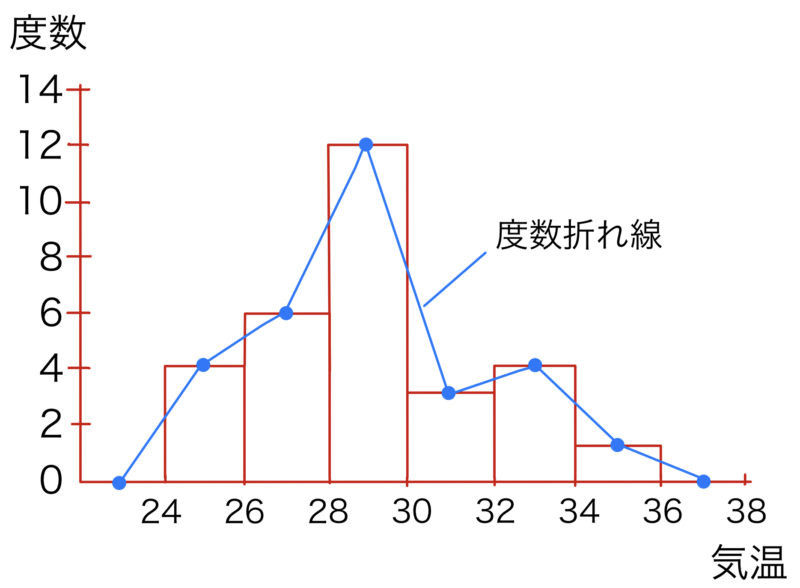
最後に,記事の中でも登場したスタージェスの公式を紹介しておく.
観測値の総数を$n$としたとき,階級の数$C$の目安は
$$C=1+\frac{\log n}{\log 2}\fallingdotseq 1+3.3\log_{10}n$$
で表される.ここで真ん中辺の分母分子$\log$は底が$e=2.71\cdots$の自然対数を表す.
スタージェスの公式によれば,観測値の総数$n$と階級の数$C$の目安は次のようにまとめられる.
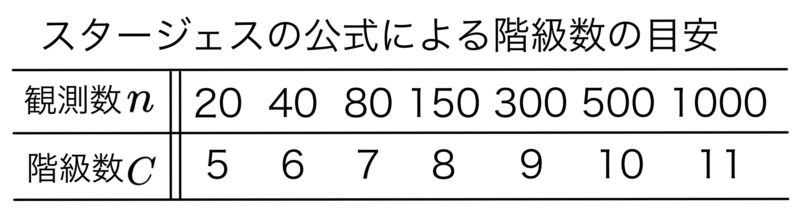
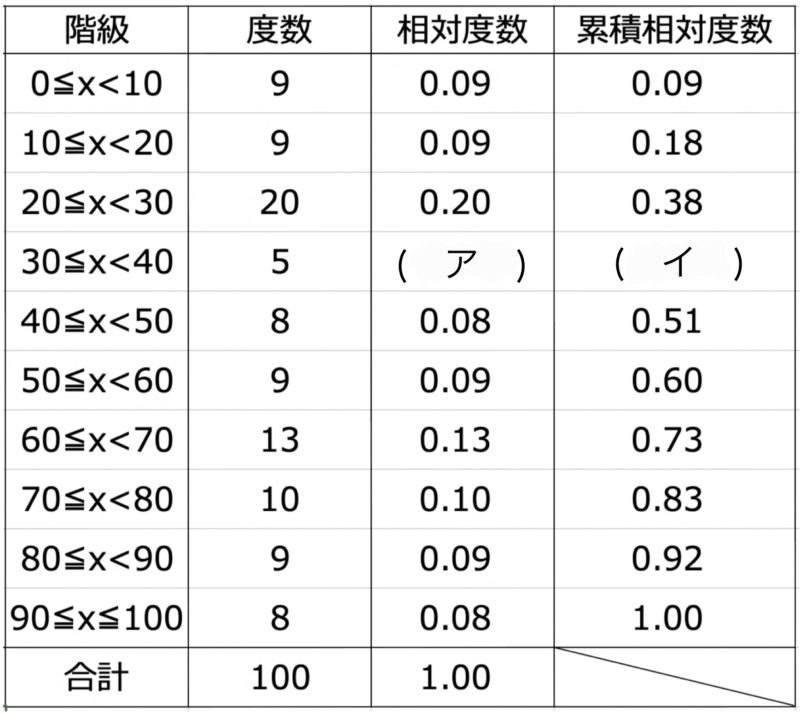
100人の学生に対し100点満点のテストを行い,その結果を以下の度数分布表にまとめた.( )に適する数値を求めよ.
この範囲のテキスト試読はこちら
この記事の動画解説版はこちら↓
| 前の記事へ戻る 01 変数の分類 |
次の記事へ 03 平均 |
| 記事一覧へ戻る 統計学の基礎シリーズ 目次 |
|

