この記事の動画解説版はこちら→統計チャンネル
※$\chi^2$分布,$F$分布の本来の定義はおまけ編で扱う.
不偏分散の分布(1標本)
確率変数$X_1, X_2, \cdots , X_n$は互いに独立で,平均$\mu$,分散$\sigma^2$の母集団分布に従うとする.このとき次の統計量は自由度$n-1$の $\chi^2$ 分布とよばれる分布に従うことが知られている(おまけ編参照).
$ \displaystyle \sum_{i=1}^{n}\frac{(X_i-\overline{X})^2}{\sigma^2}=\frac{(n-1)U^2}{\sigma^2}\sim\chi^2(n-1)$
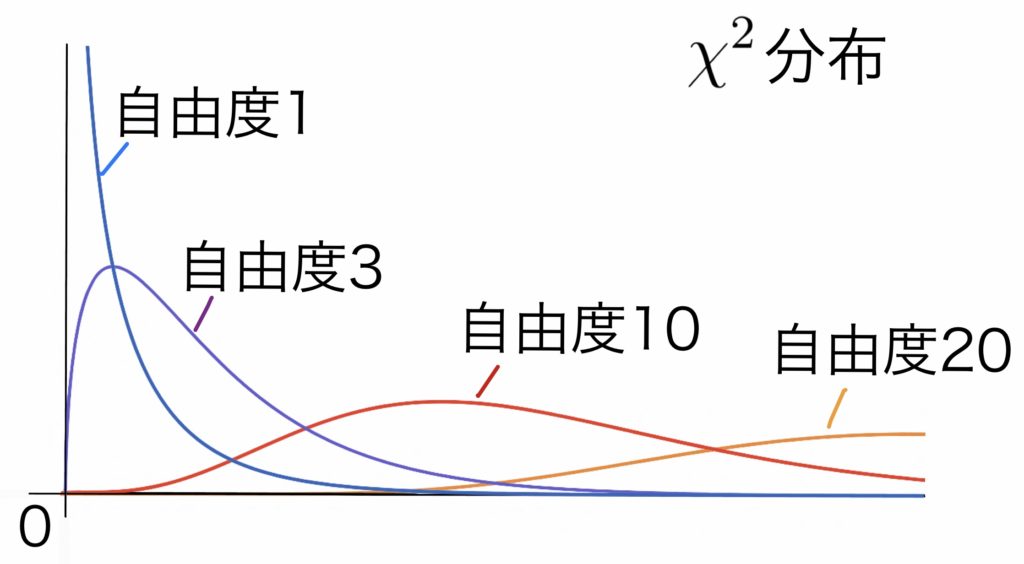
統計量分子の$(n-1)U^2$は標本平均との偏差$X_i-\overline{X}$の平方和を表していることに注意しておこう.

不偏分散の分布(2標本)
確率変数 $ \displaystyle X_1, X_2, \cdots , X_{n_A}$,$Y_1, Y_2, \cdots , Y_{n_B}$ は互いに独立で,
$ \displaystyle X_1, X_2, \cdots , X_{n_A}$は平均$\mu_A$,分散 $\displaystyle {\sigma_{A}}^{\!2}$の正規分布に従い,
$Y_1, Y_2, \cdots , Y_{n_B}$ は平均$\mu_B$,分散 $\displaystyle {\sigma_{B}}^{\!2}$の正規分布に従うとする.
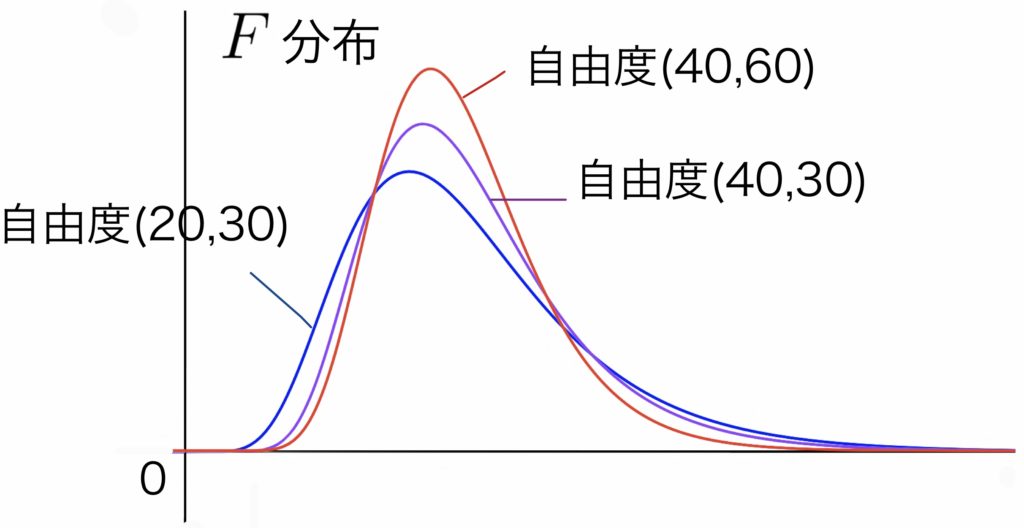
このとき次の統計量は自由度$\displaystyle (n_A-1, n_B-1)$の $F$ 分布とよばれる分布に従うことが知られている(おまけ編参照).
$\displaystyle \frac{\left(\sum_{i=1}^{n_A}\frac{(X_i-\overline{X})^2}{{\sigma_{A}^{ 2}}}\right)/(n_A-1)}{\left(\sum_{i=1}^{n_B}\frac{(Y_i-\overline{Y})^2}{{\sigma_{B}^{ 2}}}\right)/(n_B-1)}$
$\displaystyle =\frac{{U_{A}}^2/{\sigma_{A}}^2}{{U_{B}}^2/{\sigma_{ B}}^2}\sim F(n_A-1, n_B-1)$
次の文章について,$( \ \ )$に最も適する語句をそれぞれ選択肢から選べ.
$\displaystyle X_1, X_2, \cdots , X_{16}$は平均$\mu_A$,分散${\sigma_A}^2$の正規母集団からの無作為標本,
$\displaystyle Y_1, Y_2, \cdots , Y_{11}$は平均$\mu_B$,分散${\sigma_B}^2$の正規母集団からの無作為標本とし,
$\displaystyle \overline{X}=\frac{1}{16}\sum_{i=1}^{16}X_i$,$\displaystyle \overline{Y}=\frac{1}{11}\sum_{i=1}^{11}Y_i$,
$\displaystyle {U_A}^2=\frac{1}{15}\sum_{i=1}^{16}(X_i-\overline{X})^2$, $\displaystyle {U_B}^2=\frac{1}{10}\sum_{i=1}^{11}(Y_i-\overline{Y})^2$
と定める.
(1) $\displaystyle X_1, \cdots, X_{16}$について,標本平均との偏差平方和と$\sigma^2$との比
$\displaystyle \hspace{5mm}\chi^2=\frac{1}{{\sigma_A}^2}\sum_{i=1}^{16}(X_i-\overline{X})^2=\frac{15{U_A}^2}{{\sigma_A}^2}$
は自由度( $\mbox{①}$ )の$\chi^2$分布に従う.$\chi^2$が( $\mbox{②}$ )から( $\mbox{③}$ )の間の値をとる確率は約$95\%$である.
(2) $Y_1, \cdots, Y_{11}$についても(1)と同様な量$\displaystyle \frac{10{U_B}^2}{{\sigma_B}^2}$を考え,それぞれの自由度で割った統計量の比
$\hspace{5mm}\displaystyle F=\frac{\frac{15{U_A}^2}{{\sigma_A}^2}/15}{\frac{10{U_B}^2}{{\sigma_B}^2}/10}=\frac{{U_A}^2/{\sigma_A}^2}{{U_B}^2/{\sigma_B}^2}$
は${U_A}^2,{U_B}^2$が独立のとき,自由度( $\mbox{④}$ )の$F$分布に従う.$F$が( $\mbox{⑤}$ )以上の値をとる確率は約$5\%$である.
【選択肢】$15, \ 16,\ (15,10),\ (16,11),$
$ 2.85,\, 3.25,\ 6.26,\ 10.24,\ 27.49 $
この記事の動画解説版はこちら↓
| 前の記事へ戻る 37 標本平均の分布 |
次の記事へ 39 区間推定の一般的な手順 |
| 記事一覧へ戻る 統計学の基礎シリーズ 目次 |
|

