区間推定の一般的な手順

この記事の動画解説版はこちら→統計チャンネル

推定量に実現値を代入して得られた推定値は，一般に母数とズレが生じる．そこで，推定量の確率分布をもとにして，推定値を幅をもった区間として表現しようとするのが区間推定である．例題を通して，区間推定の手順を紹介する．

(例)機械Aが製造するある部品の重量は平均$\mu$ (g)，分散$\sigma^2=0.7^2$の正規分布に従うことが知られている．この部品について$7$個を無作為に選び，重量(g)を計測すると，以下の通りとなった．平均$\mu$の$95\%$信頼区間を求めよ．

(STEP 0) 最初に信頼係数を設定

「$95\%$信頼区間を求めよ」との問題文の指定により，信頼係数は$95\%$とする．(STEP3の区間の計算で基準として用いる)

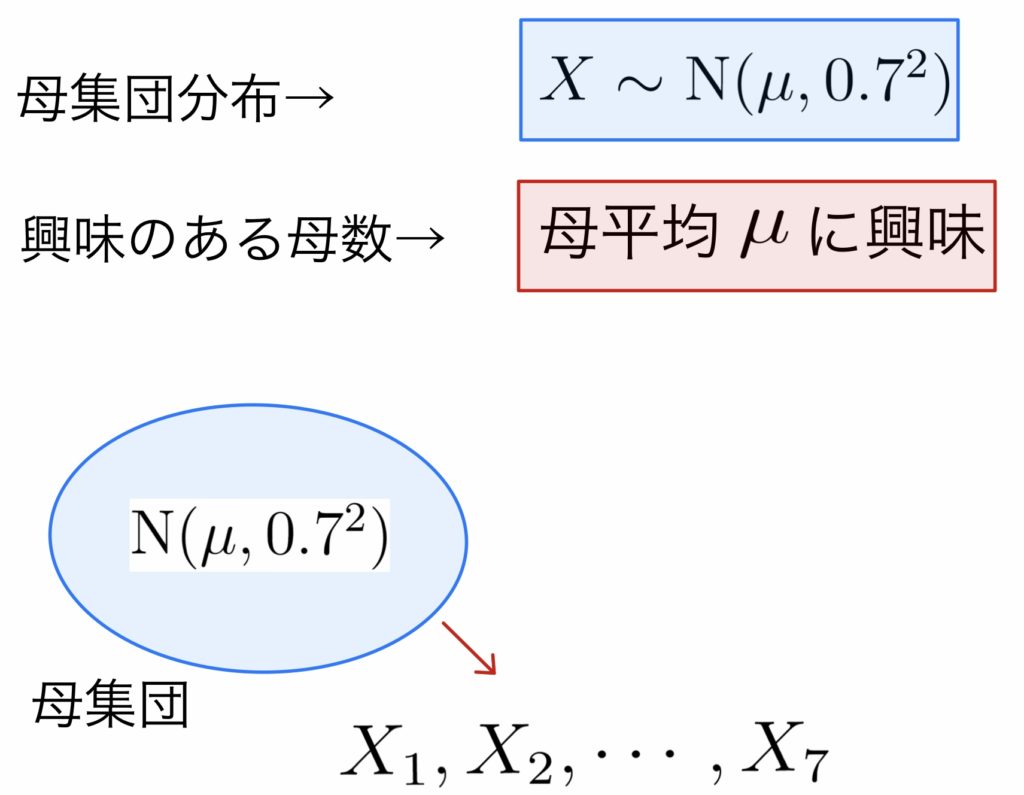
(STEP1) 母集団分布と，興味のある母数の確認

今回の母集団分布は正規分布$\mbox{N}(\mu, 0.7^2)$，最終的には$\mu$が知りたいという状況である．

(STEP 2)興味のある母数を含む統計量の分布を調べる

今回は平均重量(母平均$\mu$)に興味があるので，標本平均の分布を確認する．

　$ \displaystyle　\overline{X}=\frac{X_1+X_2+\cdots +X_7}{7}\sim \mbox{N}\left(\mu, \frac{\sigma^2}{7}\right)$

標準化すれば $ \displaystyle Z=\frac{\overline{X}-\mu}{\sqrt{\sigma^2/7}}\sim \mbox{N}(0,1)$

(STEP 3)区間を計算

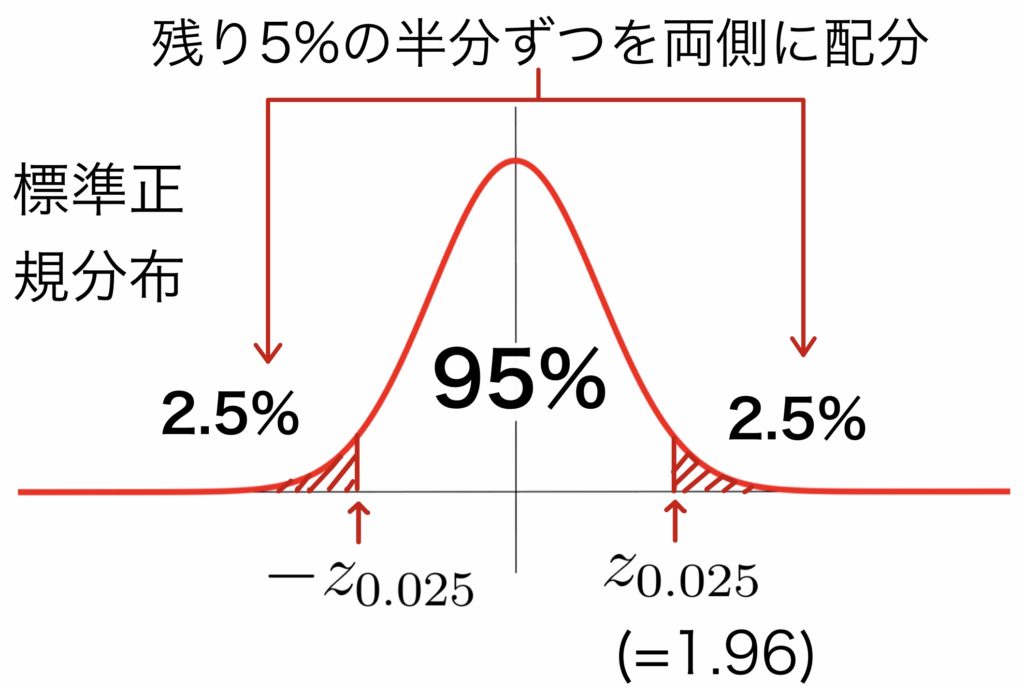
信頼係数$95\%$の残り$5\%$を上記分布$\mbox{N}(0,1)$の両側に半分ずつ配置し，「統計量(今回の場合$Z$)が$95\%$の場所に分布すること」を不等式で表す．

　$ \displaystyle -1.96\leqq \frac{\overline{X}-\mu}{\sqrt{\sigma^2/7}}\leqq 1.96$

興味のある母数について解く
　$ \displaystyle \overline{X}-1.96\sqrt{\frac{\sigma^2}{7}}\leqq \mu\leqq \overline{X}+1.96\sqrt{\frac{\sigma^2}{7}}$
実現値$ \displaystyle \overline{x}=9.8$および与えられた条件$ \displaystyle \sigma^2=0.7^2$ を代入して計算
　$ \displaystyle 9.8-1.96\sqrt{\frac{0.7^2}{7}}\leqq \mu\leqq 9.8+1.96\sqrt{\frac{0.7^2}{7}}$
すなわち，求める$95\%$信頼区間は $ \displaystyle 9.3\leqq \mu \leqq 10.3$ (終わり)

問

ある中学校の生徒10人を無作為に選び，学力試験を行ったところ，次のような結果になった．この中学校の学力試験の点数分布は正規分布に従うと仮定して，次の問いに答えよ．

(1)標本から得られた不偏分散$191.4$を母分散とみなす場合の，母平均$\mu$の$95\%$信頼区間として最も適当なものを選択肢から選べ．
(2)母分散が未知として母平均$\mu$の$95\%$信頼区間を求めよ．
【選択肢】
$ \mbox{①}\, 46.5\leqq\mu\leqq 61.3\ \ \mbox{②}45.9\leqq\mu\leqq 61.9$
$\mbox{③} \, 45.3\leqq\mu\leqq 62.5 \mbox{④}\, 44.7\leqq\mu\leqq 63.1$
$ \mbox{⑤}\, 44.0\leqq\mu\leqq 63.8$

本ブログ・解説動画に対応した資料です(note)

この記事の動画解説版はこちら↓