標本平均の分布

この記事の動画解説版はこちら→統計チャンネル

※$t$分布の本来の定義はおまけ編で扱う．

確率変数$X_1, X_2, \cdots , X_n$は互いに独立に平均$\mu$，分散$\sigma^2$の母集団分布に従うとする．標本平均$\displaystyle \overline{X}=\frac{1}{n}\sum_{i=1}^{n}X_i$について，
$\hspace{5mm} \displaystyle E(\overline{X})=\mu,\ \ V(\overline{X})=\frac{\sigma^2}{n}$
が成り立つ．また，以下のことも成り立つ．

(1) 母集団分布各$i$で$\displaystyle X_i\sim N(\mu, \sigma^2)$のとき，正規分布の再生性により
　$n$の大きさに関わらず $\displaystyle \overline{X}\sim N\left(\mu, \frac{\sigma^2}{n}\right)$

(2) 母集団分布に仮定がないとき，中心極限定理により
　$n$が十分大きければ近似的に$\displaystyle \overline{X}\sim N\left(\mu, \frac{\sigma^2}{n}\right)$
　標準化すれば$\displaystyle \frac{\overline{X}-\mu}{\sqrt{\sigma^2/n}}\sim N(0,1)$

(3) $\ \displaystyle \frac{\overline{X}-\mu}{\sqrt{\sigma^2/n}}\sim N(0,1)$のとき，$\sigma^2$を不偏分散
$\hspace{5mm}\displaystyle U^2=\frac{1}{n-1}\sum_{i=1}^{n}(X_i-\overline{X})^2$
に取り替えた統計量は自由度$n-1$の$t$分布とよばれる分布に従うことが知られている(おまけ編参照)．
$\hspace{5mm}\displaystyle \frac{\overline{X}-\mu}{\sqrt{U^2/n}}\sim t(n-1)$

$t$分布は自由度を大きくすると標準正規分布に近づくような分布である．

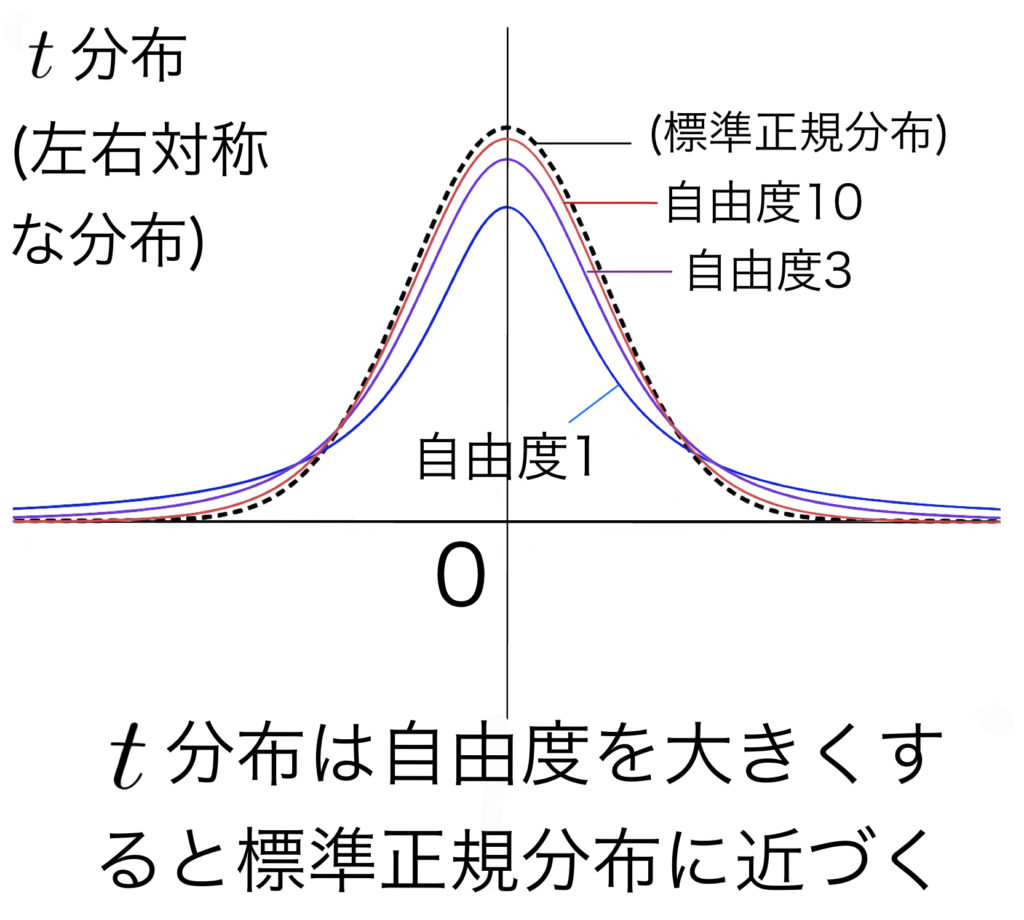
$t$分布については，自由度ごとの上側確率(よく使うもの)が数表としてまとめられている．

本ブログ・解説動画に対応した資料です(note)

この記事の動画解説版はこちら↓