平均

この記事の動画解説版はこちら→統計チャンネル

①すべての観測値$x_1,x_2,\cdots , x_n$が与えられているときの平均$\overline{x}$は$$\overline{x}=\frac{1}{n}(x_1+x_2+\cdots +x_n)$$で定義される．この右辺はシグマ記号$\sum$を用いて$$\overline{x}=\frac{1}{n}\sum_{i=1}^{n}x_i $$のようにも表される．

②度数分布表が与えられた場合の平均

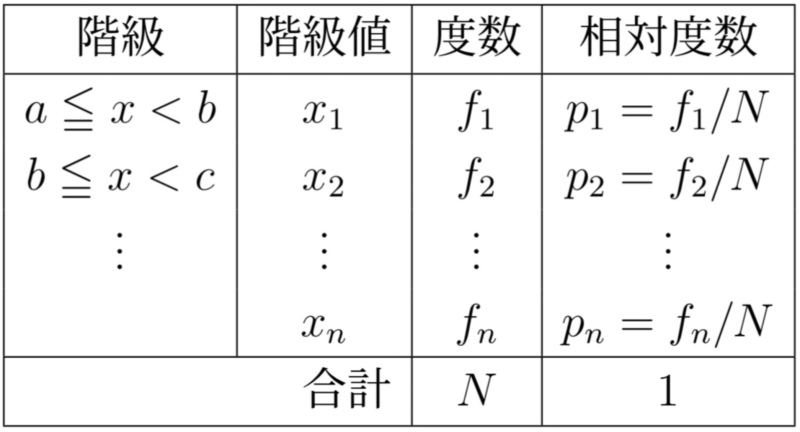
度数分布表では整理する際に情報の一部が失われているため，もとになる観測値の平均を計算することはできない．度数分布表からの平均は，その階級に属する観測値がすべて階級値をとったものとして計算する．上の表の記号でいうと，平均は次のように計算すればよい．$$\overline{x}=\frac{1}{N}(x_1f_1+x_2f_2+\cdots+x_nf_n)$$

この緑線がついた部分の式変形は，確率変数の話で使うために行っているもので，現時点では軽く聞き流す程度に見てもらえればOK．

度数分布表から計算する平均は，シグマ記号を用いると，次のように表される．

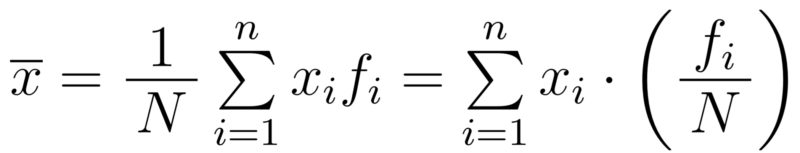
右辺の最後の式は(相対度数×階級値)の和になっていることに注意しよう．この事実をもとに確率変数の期待値と呼ばれる概念が定義される(記事17で扱う)．

具体的に，度数分布表から平均を計算してみよう．

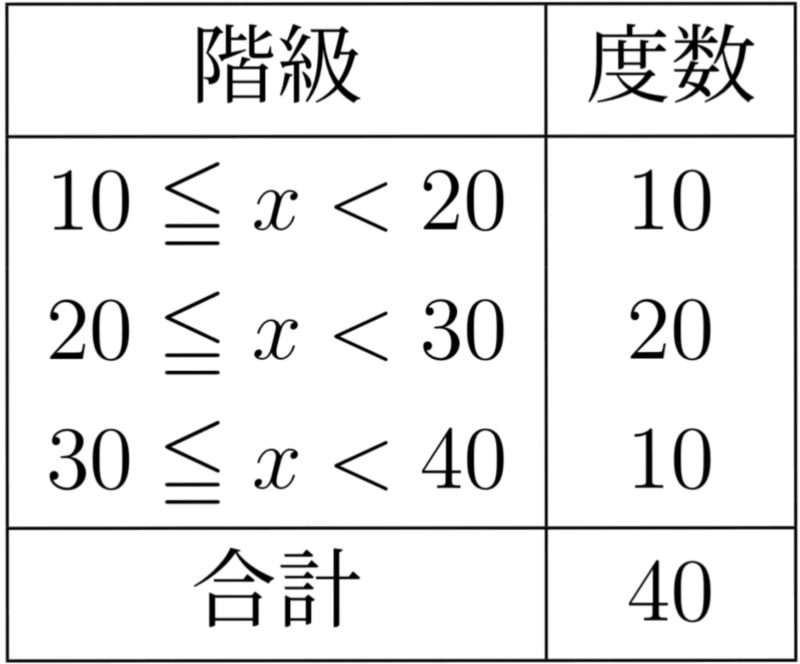
階級に属する観測値は，それぞれ階級値をとったものとして計算するのだから，平均は以下のようになる．

$$\overline{x}=\frac{1}{40}(15\cdot 10+25\cdot20+35\cdot 10)=25$$

本ブログ・解説動画に対応した資料です(note)

この記事の動画解説版はこちら↓