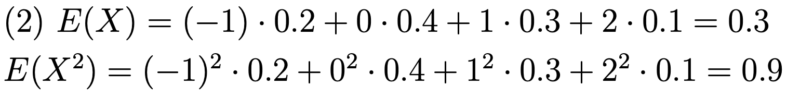確率変数

この記事の動画解説版はこちら→統計チャンネル

確率変数

以下の条件を満たす変数を確率変数という．

①試行の結果，実現値が定まる
②各実現値に応じた確率が考えられる

確率変数のとりうる値とそれぞれの確率をまとめたものを確率分布という．確率分布は表、あるいは式の形で表現されることが多い．確率変数には離散型と連続型があるが，しばらくは離散型の確率変数に絞って話をすすめていく．

例えば，1個のサイコロを投げた投げるとき，その出る目を$X$とすると，確率分布は以下のように表現される．

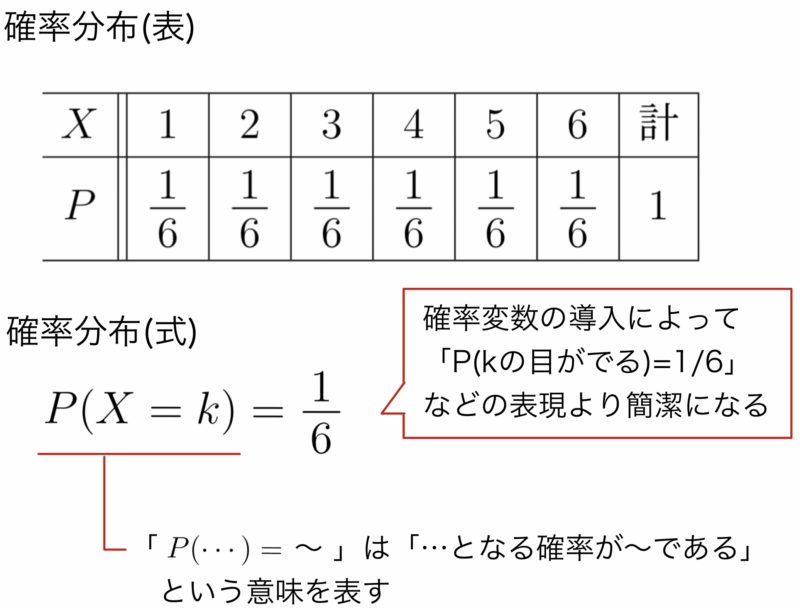
期待値

サイコロをたくさん投げるのを想像してみよう．例えばサイコロを6万回ぐらい投げれば，1から6の目がそれぞれ約1万回ずつ出ると期待できる．これは試行数$N$を十分大きくして度数分布表を作成したとき，$X=1, X=2,\cdots , X=6$に対応する相対度数が，それぞれ確率$p_1=\frac16, p_2=\frac16, \cdots, p_6=\frac16$ と近い値をとることを意味する．すなわち，試行数$N$が十分大きければ，確率変数$X$が$x_i$となる結果の相対度数は，確率$p_i=P(X=x_i)$に近づくと考えられる．このことから，確率変数版の平均(確率変数の場合は期待値ともいう)が次のように定義される．

度数分布表での平均の式(記事03参照)は次のように定義された．

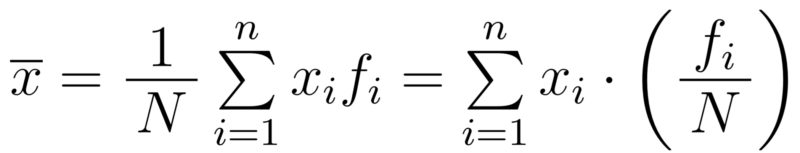
すでに述べたように，$N$を十分大きくすれば相対度数$f_i/N$ は 確率$p_i=P(X=x_i)$に近づくと考えられる．そこで，確率変数の期待値(平均) $E(X)$を次のように定義する．

$X$の関数$\varphi(X)$に対してその期待値$E(\varphi(X))$を次のように定義する．

$$\varphi(X))=\sum_{i=1}^{n}\varphi(x_i)p_i$$

先ほどのサイコロの例では，$E(X), E(X^2)$は以下のように計算される．

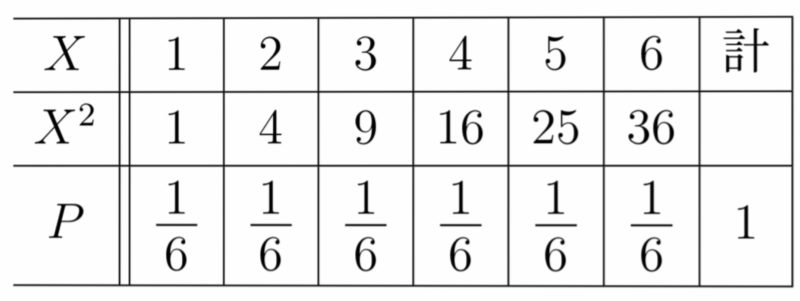
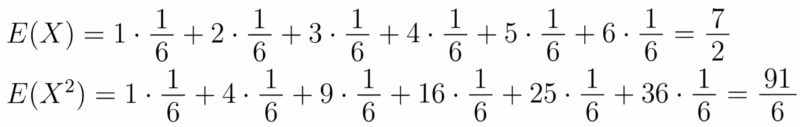
期待値については，次のような性質がある．

$a,b,c$を定数，$\varphi(X), \psi(X)$を$X$の関数とする．
(1) $E(c)=c\ $($c$は定数)
(2) $E(a\varphi(X)+b\psi(X))=aE(\varphi(X))+bE(\psi(X))$

問

確率変数$X$の分布が以下のように与えられているとする．

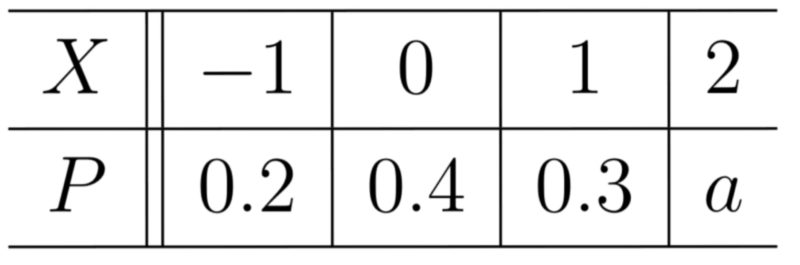
(1) $a$の値を求めよ．
(2)  $E(X), E(X^2) $を求めよ．

解答はこちら

解

(1) 確率の総和は1であるから$0.2+0.4+0.3+a=1$により $a=0.1$

本ブログ・解説動画に対応した資料です(note)

この記事の動画解説版はこちら↓