確率変数の分散

この記事の動画解説版はこちら→統計チャンネル

確率変数の分散$V(X)$を次のように定義する．

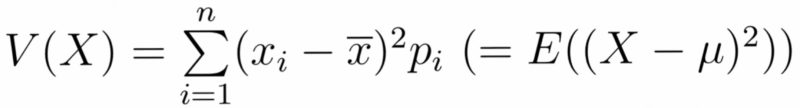
分散は$\sigma^2$という記号でも表される．また，$\sigma=\sqrt{V(X)}$を標準偏差という．

(例)サイコロを投げるときの出る目を$X$とする(以下，「サイコロの例」と呼ぶことにする)．平均は$\displaystyle E(X)=\frac72$であったから，分散は

となる．

確率変数の分散について，記述統計編の分散と同様な以下の公式がある．

上の証明は定義に基づいたものであるが，前回記事の期待値の性質から

　$\displaystyle E((X-\mu)^2)=E(X^2-2\mu X+\mu^2)$
　　$\displaystyle =E(X^2)-2\mu\cdot \mu +\mu^2$
　　$\displaystyle =E(X^2)-\mu^2$

のように導くこともできる．

サイコロの例で，前回記事で扱ったように\( \displaystyle E(X^2)=\frac{91}{6} \)であったから，分散は公式から

　$\displaystyle V(X)=E(X^2)-(E(X))^2$
　　　\( \displaystyle =\frac{91}{6}-\left(\frac72\right)^2=\frac{35}{12} \)

とも計算できる(もちろん定義から計算した場合と同じ値となる)．

確率変数$X$の一次式$aX+b$ ($a,b$は定数)の期待値と分散について，記述統計編の分散と同様な以下の公式がある．

(証明) 定義に従って示す．シグマの性質を用いればよい．

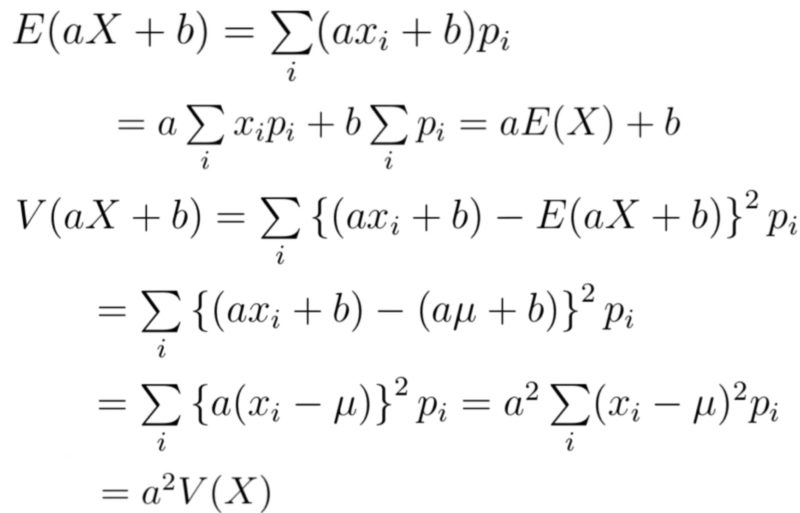
(期待値の性質から示すこともできる)

サイコロの例について，$3X+1$の平均と分散は

　　$ \displaystyle E(3X+1)=3E(X)+1=3\cdot \frac72+1=\frac{23}{2}$

　　$ \displaystyle V(3X+1)=3^2V(X)=9\cdot \frac{35}{12}=\frac{105}{4}$

本ブログ・解説動画に対応した資料です(note)

この記事の動画解説版はこちら↓