回帰直線

この記事の動画解説版はこちら→統計チャンネル

回帰直線

変数$y$を$x$の一次式で説明するモデルを考える(単回帰モデル)$$y=\alpha +\beta x$$

観測値$(x_i, y_i)\ (i=1,2,\cdots , n)$に対して

$$Q(\alpha, \beta)=\sum_{i=1}^{n}\{y_i-(\alpha+\beta x_i)\}^2$$

を最小にする$\alpha, \beta$として以下の値が求まることが知られている(最小二乗法)．

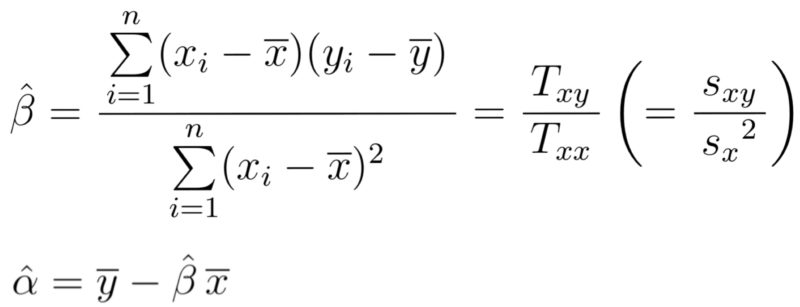
$y=\hat{\alpha}+\hat{\beta}x$を回帰式または回帰直線という．上の第二式は回帰直線が$(\overline{x}, \overline{y})$を通ることを意味する．回帰式による $ y_i $ の推定値を$$\hat{y_i} (=\hat{\alpha}+\hat{\beta}x_i)$$と表す．

具体的な例で回帰直線を求めてみよう．

(例) 10人の男子大学生の身長(x cm)と右足の大きさ(y cm)を測定すると，次のようになった．なお，xとyの共分散の値は9.28である．

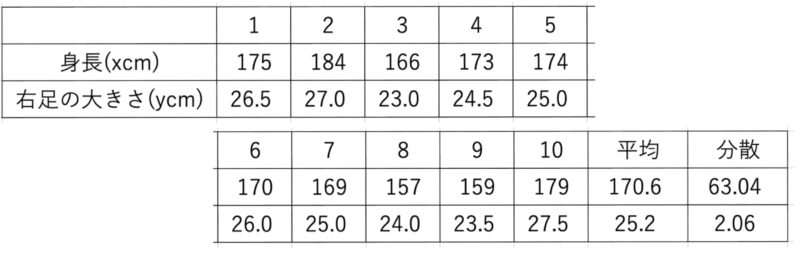
実際に先ほどの式から$\hat{\beta}, \hat{\alpha}$を計算すると

であるから回帰直線は$y=0.0860+0.14721x$となる．実際の散布図，回帰直線以下のようになる．

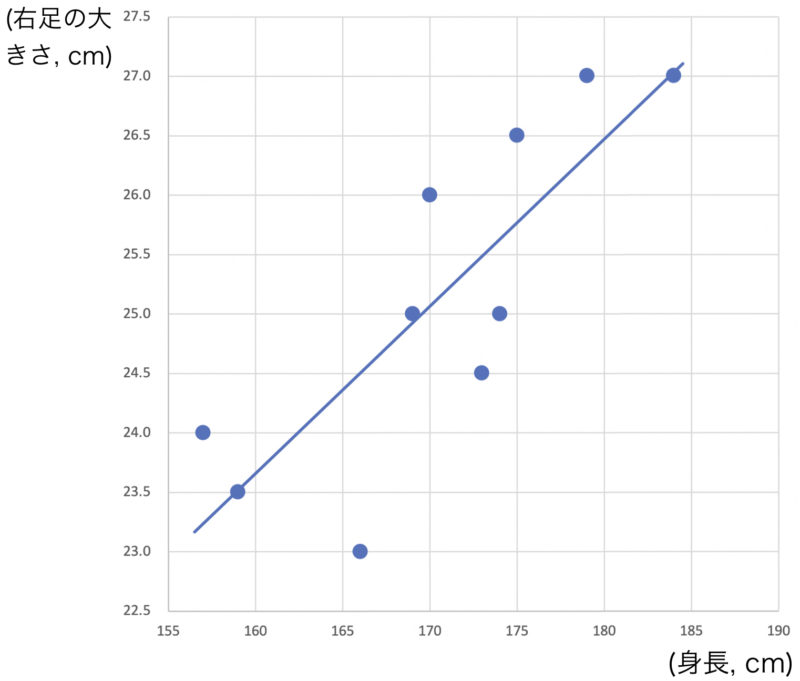
また，回帰直線によって，身長190cmの男子大学生の右足の大きさを推定すると$$y=0.0860+0.14721\cdot 190\fallingdotseq 28.1(\mbox{cm})$$となる．このように，回帰式を用いて$x$が特定の値のときの$y$の値を推定することがある．

決定係数

ここからは，回帰直線の当てはまりぐあいを数値化することを考える．

$y$の偏差の二乗和 $S_T=\sum_{i=1}^{n}(y_i-\overline{y})^2$ を総平方和という．総平方和$S_T$は次のように分解できることが知られている．

$$S_T=\sum_{i=1}^{n}(\hat{y_i}-\overline{y})^2+\sum_{i=1}^{n}(y_i-\hat{y_i})^2$$

この第一項を回帰平方和$S_R$といい，第二項を残差平方和$S_E$という．

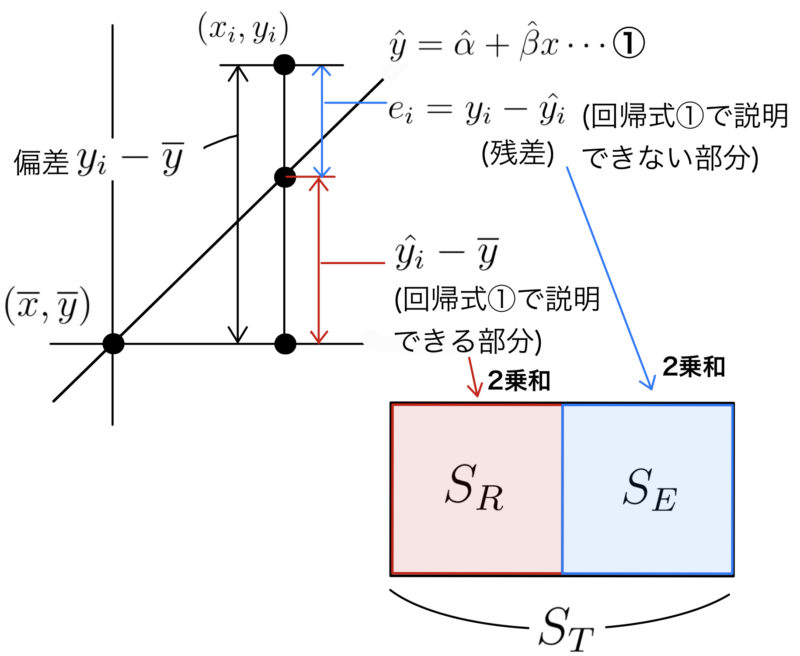
観測値への回帰直線の当てはまりがよければよいほど，$S_T$に対する$S_R$の割合は大きくなると考えられる．そこで回帰直線の当てはまりのよさとして，次の決定係数$R^2$が定義される．

決定係数は $0\leqq R^2 \leqq 1$ を満たす．また，決定係数$R^2$は$x,y$の相関係数の2乗${r_{xy}}^2$と等しいことが知られている．

先ほどの男子大学生の身長と右足のサイズについては，相関係数が$$r_{xy}=\frac{s_{xy}}{s_xs_y}=\frac{9.28}{\sqrt{63.04\cdot 2.06}}=0.8143\cdots$$と求まるので，決定係数は$$R^2={r_{xy}}^2=(0.8143\cdots)^2\fallingdotseq 0.663$$となる(このことから，回帰直線は観測値の66.3%程度を説明しているなどと表現することがある)．

自由度修正済み決定係数

変数$y$を$k$個の変数$x_1, x_2, \cdots, x_k$で説明するモデルを考える(重回帰モデル)．$$y=\alpha+\beta_1x_1+\beta_2x_2+\cdots +\beta_{k}x_k$$

一般に，説明変数を増やすとその説明変数の妥当性にかかわらず，決定係数は増大する．説明変数の個数の異なるモデルの比較のためには，次の自由度修正済み決定係数$R^{*2}$が用いられる．

$$R^{*2}=1-\frac{S_E/(n-k-2)}{S_T/(n-1)}$$

この範囲のテキスト試読はこちら

本ブログ・解説動画に対応した資料です(note)

この記事の動画解説版はこちら↓