散布図,相関係数

この記事の動画解説版はこちら→統計チャンネル

2つの変数からなる組のデータ$(x_i, y_i)\ (i=1,2,\cdots n)$をプロットしたグラフを散布図という．一方の変数が増加すると他方の変数も増加する傾向にあるとき、変数間に正の相関関係があるという．また，一方の変数が増加すると他方の変数が減少する傾向にあるとき，変数間に負の相関係数があるという．

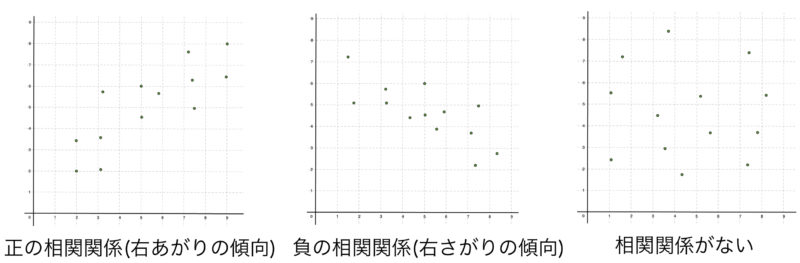
相関の強さを数値化することを考える．下図のように，2つの直線$x=\overline{x}, y=\overline{y}$で散布図を4つの領域①〜④に分ける．

正の相関関係があるときは①または③の領域に点が多くなり，負の相関関係があるときは②または④の領域に点が多くなることが期待される．また，$x,y$の偏差の積$(x_{i}-\overline{x})(y_i-\overline{y})$　について，

点$(x_i, y_i)$ が①または③に属するときは$(x_{i}-\overline{x})(y_i-\overline{y})>0$

点$(x_i, y_i)$ が②または④に属するときは$(x_{i}-\overline{x})(y_i-\overline{y})<0$

であるから，次の共分散$s_{xy}$(偏差の積の平均)は正の相関関係があるときは正の値をとり，負の相関関係が負の値をとることが期待できる．

$$s_{xy}=\frac{1}{n}\sum_{i=1}^{n}(x_i-\overline{x})(y_i-\overline{y}) $$

共分散は上限がなく，またデータを2倍するなどの加工で値が変動するため，相関係数の強さの比較には用いることができない．そこで，以下の相関係数$r_{xy}$がよく用いられる．

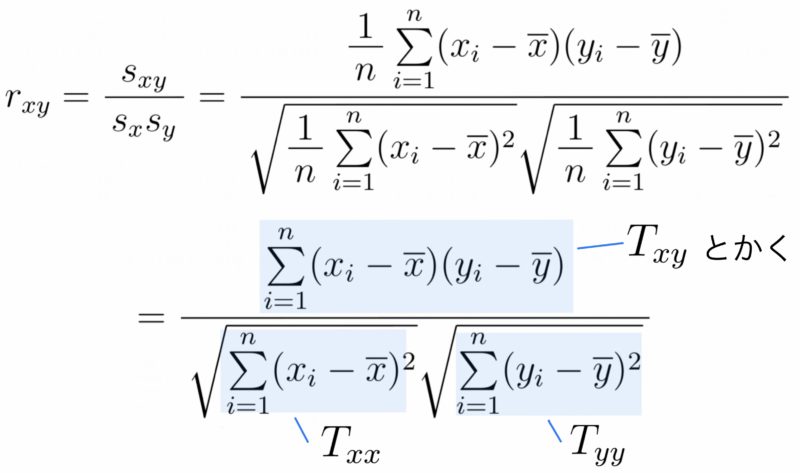
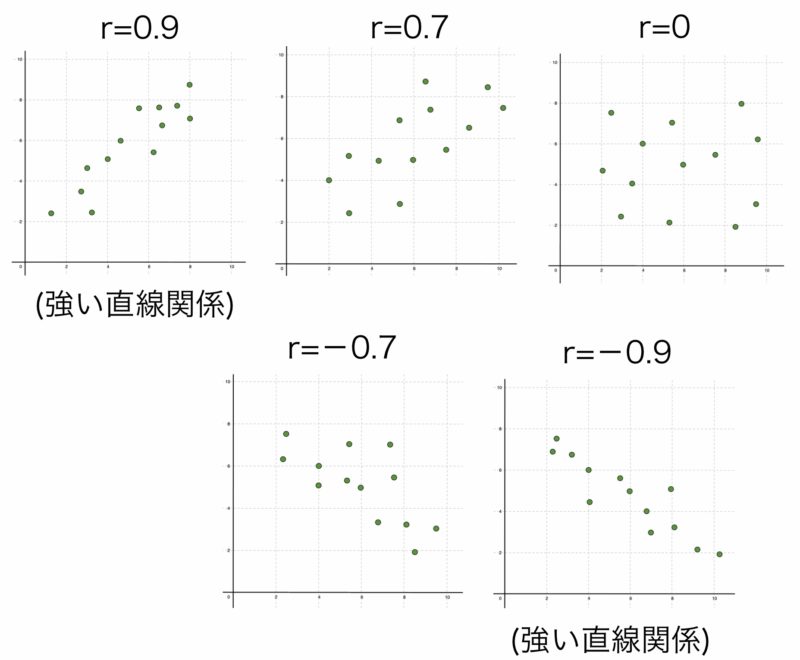
(最後の$T_{xy}. T_{xx}, T_{yy}$はあとの記事で使うので導入した記号で，それぞれ共分散，$x$の分散，$y$の分散を$n$倍したものである)．相関係数の値はつねに$-1\leqq r_{xy}\leqq 1$の範囲にあることが知られており，正の相関関係が強いほど$1$に近づき，負の相関関係が強いほど$-1$に近づく．散布図から相関係数のおおよその値を目分量で求められるとよい．

問

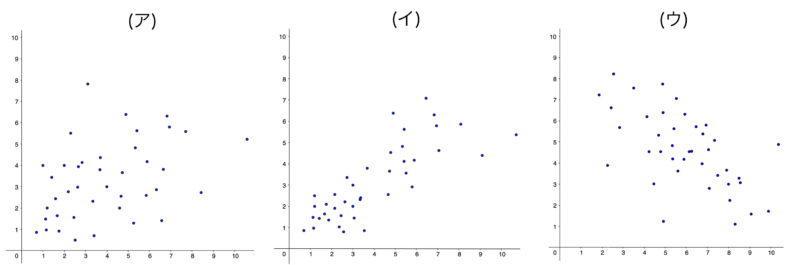
次の散布図に対応する相関係数として最も適切なものを選択肢からそれぞれ選べ．

【選択肢】$-1, -0.6, 0.4, 0.8, 1$

問

組データ$(x_i, y_i)\ (i=1,2,\cdots , n)$に対して，相関係数は次のように定義される．

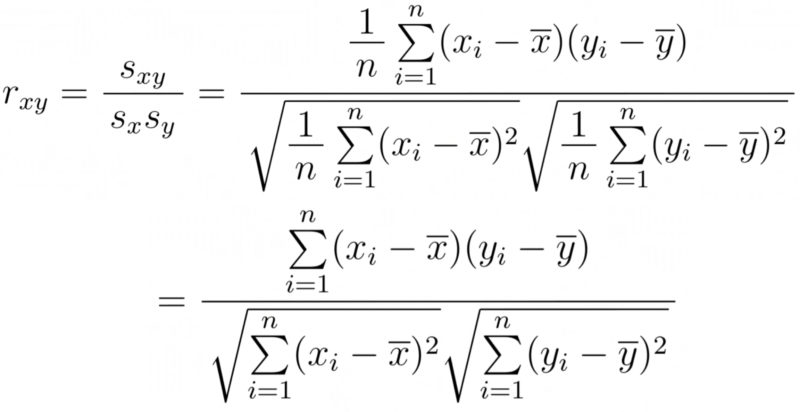
次のうち，正しいものをすべて選べ．

①各$x_i$を2倍した$(2x_i, y_i)\ (i=1,2,\cdots, n)$の相関係数は元の相関係数とつねに等しい．

②各$x_i$に1を足した$(x_i+1, y_i)\ (i=1,2,\cdots, n)$の相関係数は元の相関係数とつねに等しい．

③各$x_i$を-1倍した$(-x_i, y_i)\ (i=1,2,\cdots, n)$の相関係数は元の相関係数とつねに等しい．

④$x_i$同士の$(x_i, x_i)\ (i=1,2,\cdots, n)$の相関係数は0になる．

本ブログ・解説動画に対応した資料です(note)

この記事の動画解説版はこちら↓