ローレンツ曲線

この記事の動画解説版はこちら→統計チャンネル

格差を表現するときに，ローレンツ曲線・ジニ係数が用いられる．

例として，次のようにA社とB社にそれぞれ4人の社員がいて，年間の給与額が次のように分布しているとしよう(例なので，安すぎてブラック！となどとは言わないように)．なお，表ははじめから給与額の小さい順に並べている．

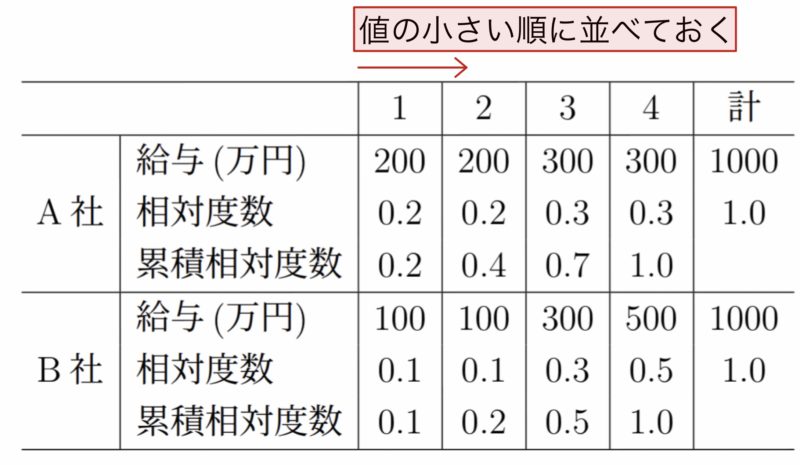
A社とB社を比較すると，B社の方がより給与の格差が大きいことがわかる．これを，次のようなローレンツ曲線とよばれる曲線で表現する．ローレンツ曲線は，横軸に構成員の数についての累積相対度数，縦軸に給与の累積相対度数をとったグラフで，完全に平等に給与が配分されている場合(今回の例の場合は1人に250万円ずつ配分されているとき)に，傾き45度の直線(完全平等線)になる．

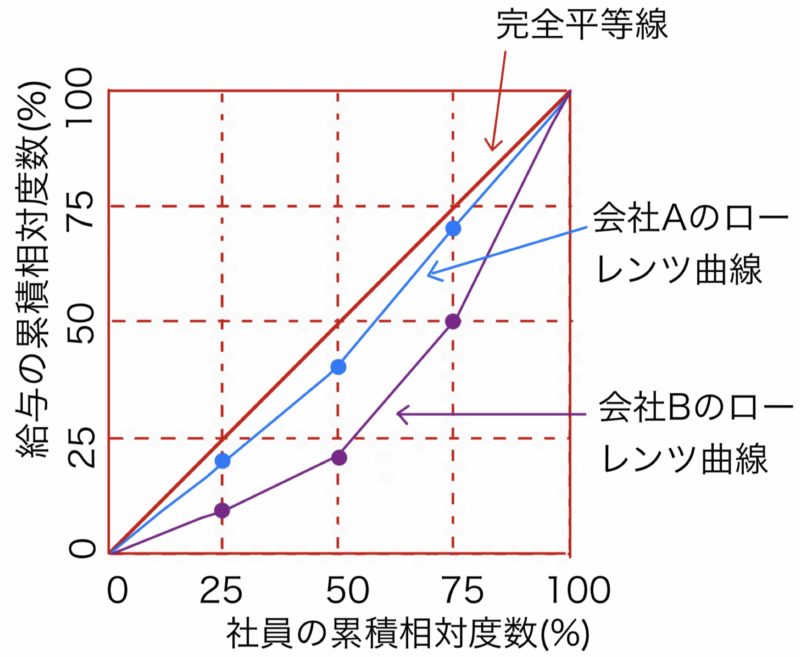
格差が大きいほど，ローレンツ曲線は完全平等線から下側に膨らむ．この例でも，会社Aよりも会社Bの方がよりローレンツ曲線が下側に膨らんでいることがわかる．

ローレンツ曲線の膨らみ具合を数値化する際に，次のジニ係数が用いられる．ジニ係数は「ローレンツ曲線と完全平等線の間の“三日月”の面積」が，「完全平等線の下にある直角三角形の面積」に占める割合であり，0以上1以下の値である．格差が小さいほど0に近く，格差が大きいほど1に近い値をとる．また，ジニ係数は縦横を長さ1の正方形と考えれば，三日月の面積の2倍として求められる．

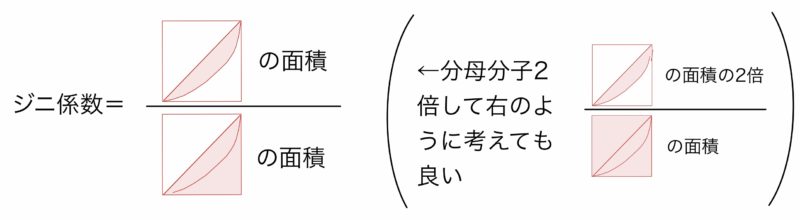
ジニ係数は単位によらない指標であり，所得の実際額の大きさの変化に依存せずに格差の大きさを評価できるので，例えば国家における格差の進行状況や，各国間での格差の比較などにも用いられる．

先ほどの例で会社Aのジニ係数を求めてみよう．全体を1辺1の正方形とみなし，“三日月”部分の面積を台形の面積公式などから計算すると，以下のようになる．

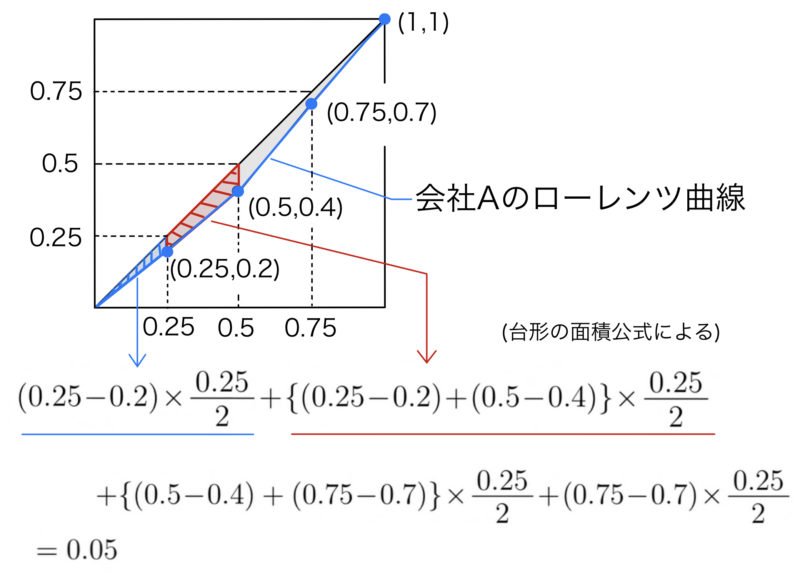
よって会社Aの給与額のジニ係数は，この三日月の面積0.05の2倍で0.10となる．同様に，会社Bの給与額のジニ係数は

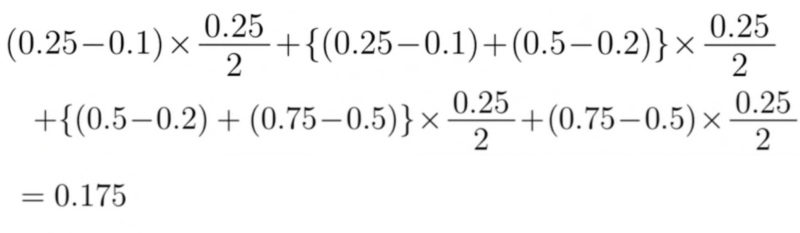
により0.175×2=0.35と計算できる．

問

平成29年の二人以上の世帯における世帯貯蓄の調査結果について，表とローレンツ曲線でまとめた．

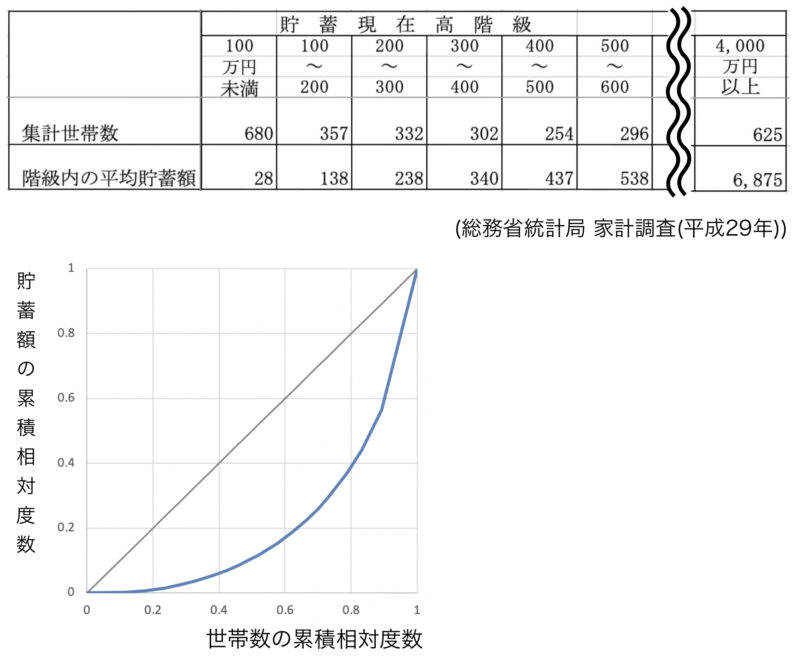
ローレン直線のグラフを1辺1の正方形とみなしたとき，ローレンツ曲線の下側に位置する領域の面積は0.21であった．このとき，ジニ係数を求めよ．

本ブログ・解説動画に対応した資料です(note)

この記事の動画解説版はこちら↓