分散と標準偏差

この記事の動画解説版はこちら→統計チャンネル

観測値の散らばり具合を表す量として，分散，標準偏差がある．

データ$x_1, x_2, \cdots, x_n$に対して，分散$v_x$は

$$v_x=\frac{1}{n}\sum_{i=1}^{n}(x_i-\overline{x})^2$$

標準偏差$s_x$は分散の平方根 $$ s_x=\sqrt{v_x}=\sqrt{\frac{1}{n}\sum_{i=1}^{n}(x_i-\overline{x})^2} $$ として定義される．分散や標準偏差の意味は，次ように考えると理解しやすい．

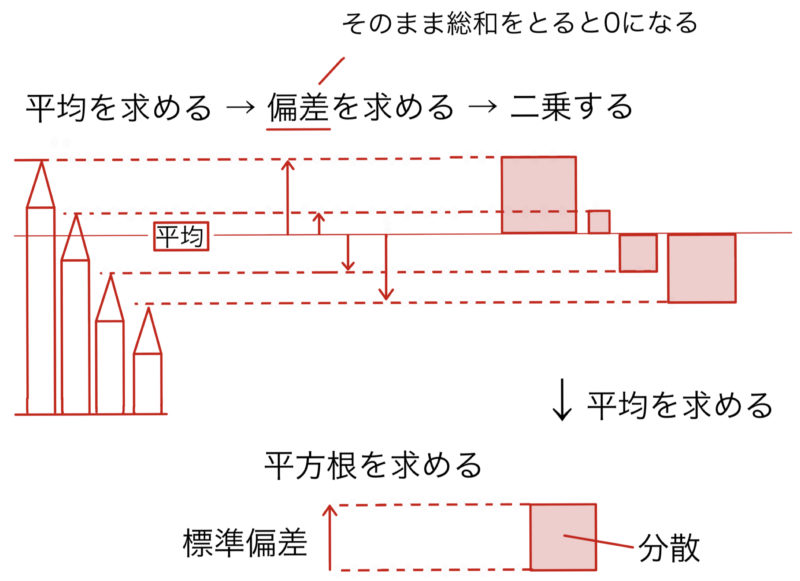
データの散らばり具合を考える際に，観測値と平均とのズレ$x_i-\overline{x}$(偏差)を考えるのは自然なことである．しかし，この偏差をそのまま合計すると常に和が$0$となって散らばりを表す量として機能しない．そこで，偏差を2乗してその平均を求めたのが分散$v_x$である．分散はもとの観測値と単位が異なる．上の例でいうと観測値の単位がcmなのに対し，分散の単位はcm²となる．このため，分散は観測値との和を計算したりすることができず不便なため，平方根をとって観測値と同じ単位になるようにしたものが標準偏差$s_x=\sqrt{v_x}$である．標準偏差は統計学で非常に重要な役割を果たす．例えば観測値が平均から標準偏差いくつぶん離れているかに応じて，その観測値の極端さを評価したりすることができる．

一つ例を扱ってみよう．

(例)データ$1,3,5,7,9$の平均，分散，標準偏差を求めよ．

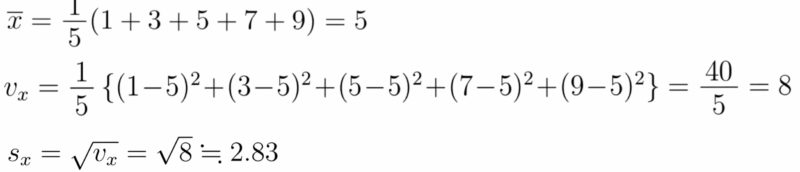
分散は，定義から求めるほかにも，以下のような計算の仕方もある．

(証明)

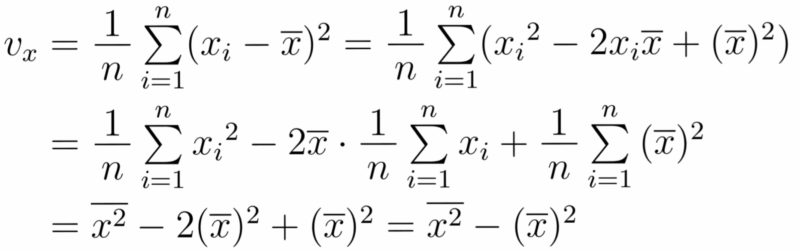
さきほどの例$ 1,3,5,7,9 $において，分散は次のように公式からも計算できる．

問

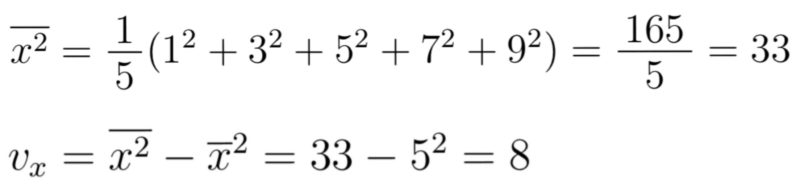
10人の男子生徒の右手の握力$x$(kg)のデータが下の表のように与えられている．握力の標準偏差を求めよ．ただし，小数第3位を四捨五入せよ．

本ブログ・解説動画に対応した資料です(note)

この記事の動画解説版はこちら↓