一次式の公式

この記事の動画解説版はこちら→統計チャンネル

もとのデータ

　$x: x_1,x_2, \cdots, x_n $

を一斉に$a$倍して$b$を足す変換をしたデータ

　$ax+b: ax_1+b,ax_2+b, \cdots, ax_n+b $

の平均$\overline{ax+b}$および分散$v_{ax+b}$は，次のように元のデータ$x$から計算できる．

(証明)

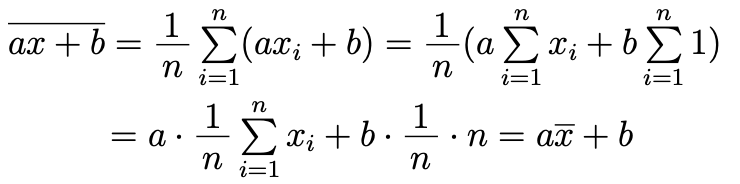
また，値$ax_i+b$の偏差，すなわち平均との差は$(ax_i+b)-(a\overline{x}+b)=a(x_i-\overline{x})$となるから，$ax+b$の分散$v_{ax+b}$ は

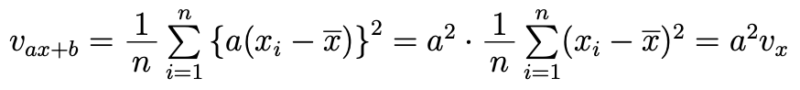
例えばデータ $1,3,5,7,9$ を一斉に2倍して1を足したデータ$3,7,11,15,19$について，

　平均は$2\times 5+1=11$，分散は$2^2\times 8=32$

となる．

解答はこちら

解

本ブログ・解説動画に対応した資料です(note)

この記事の動画解説版はこちら↓