適合度検定

この記事の動画解説版はこちら→統計チャンネル

仮定された理論上の確率分布に対して，標本から求めた度数が適合するかどうかを検証する検定を適合度検定という．

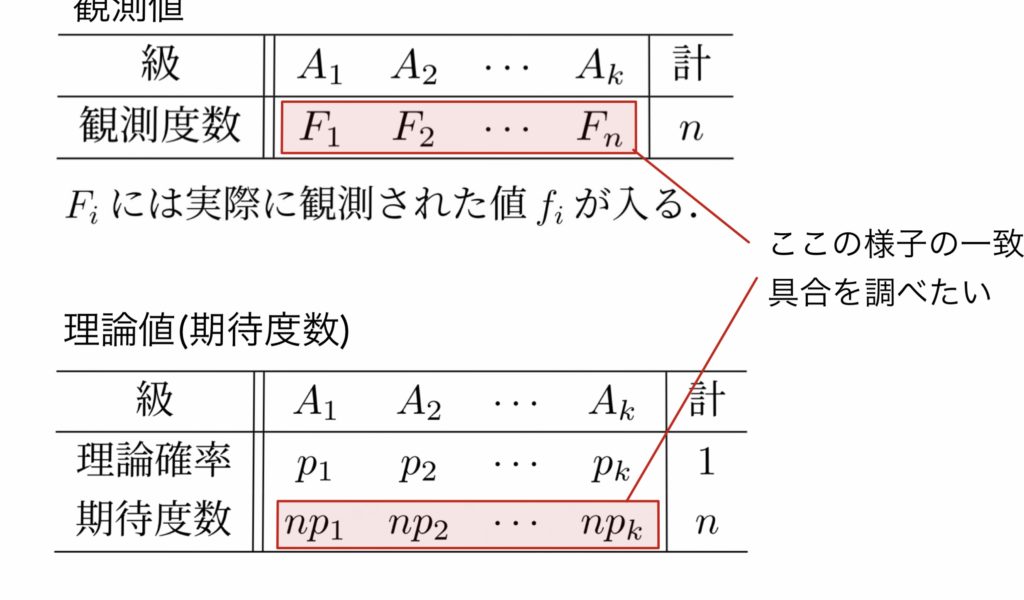
観測度数が理論確率分布に適合しているという仮説
\(\hspace{2mm}\rule[-1mm]{0mm}{7.5mm} \displaystyle H_0: P(A_1)=p_1, \cdots, P(A_k)=p_k \)
$\rule[-1mm]{0mm}{7.5mm}$のもとで，近似的に以下が成り立つことが知られている．これをもとに適合度検定を行う．
\(\hspace{5mm}\rule[-1mm]{0mm}{7.5mm} \displaystyle \chi^2=\sum_{i=1}^{k}\frac{\left(F_i-np_i\right)^2}{np_i}\sim \chi^2(k-1)\)

統計検定量は (観測値-期待度数)²/(期待度数)という形になっていることに注意しよう．

問

ある人物に，できるだけランダムに$1$ 桁の数字を$100$ 個言ってもらったところ次のような結果になった．特定の数字が多く出ている傾向にないか，有意水準$5\%$ で検定せよ．

解答はこちら

解

帰無仮説$H_0$ は「数字が一様に分布している」となる．この仮定のもとで，$0$ から$9$ までの出る確率はそれぞれ$1/10$で，期待度数はそれぞれの数字について$100×1/10=10$ となる．

(観測値-期待度数)²/(期待度数)の和は自由度$10-1=9$の$\chi^2$分布に従う．今回の棄却域は $\chi^2>\chi^2_{0.05}(9)=16.92$ である．実現値を計算すると，

\(\hspace{5mm}\rule[-1mm]{0mm}{7.5mm} \displaystyle \chi^2=\frac{(17-10)^2}{10}+\frac{(6-10)^2}{10}+\cdots +\frac{(8-10)^2}{10}=19.4(>16.62)\)

と棄却域に入るから，帰無仮説$H_0$ は棄却される．すなわち数字がランダムに述べられているとは言えないと結論する．

本ブログ・解説動画に対応した資料です(note)

この記事の動画解説版はこちら↓