この記事の動画解説版はこちら→統計チャンネル
2つの属性A,Bに対し,それぞれいくつかのカテゴリーがあり,左下のような分割表にまとめられているとする.このとき2属性A,Bの関連のなさについての検証を独立性の検定で行うことができる.

A,Bが独立であるという仮説,すなわち
$ H_0: $すべての$i,j$で$P(A_i\cap B_j)=P(A_i)P(B_j)$
のもとで,次が成り立つことが知られている.これをもとに検定を行う.
\(\hspace{3mm}\rule[-1mm]{0mm}{7.5mm} \displaystyle \chi^2=\sum_{i=1}^{r}\sum_{j=1}^{s}\frac{\left(F_{ij}-f_{i\cdot}f_{\cdot j}/n\right)^2}{f_{i\cdot}f_{\cdot j}/n}\)
\(\hspace{15mm}\rule[-1mm]{0mm}{7.5mm} \displaystyle \sim \chi^2((r-1)(s-1))\)
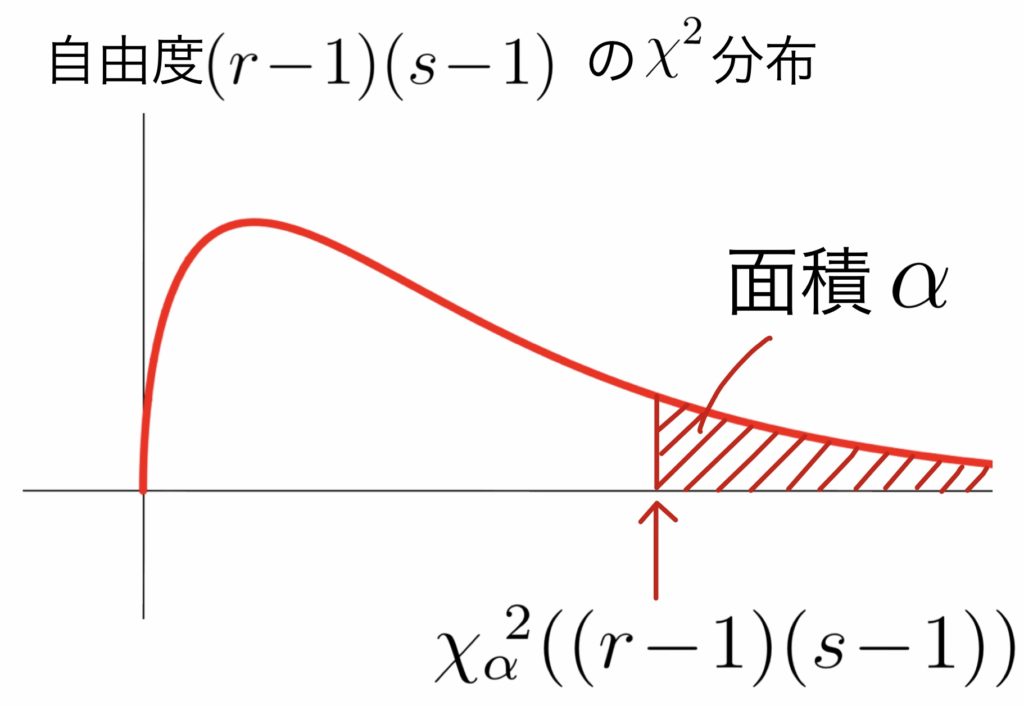
適合度検定(記事49)と同様に,ここでも統計検定量が (観測値-期待度数)²/(期待度数)という形になっていることに注意しよう.
(例)ある年において,インフルエンザの予防注射の効果を調べるため,インフルエンザにかかった人とそうでない人について,それぞれ予防注射の有無を調べ,下の表を得た.この予防注射はインフルエンザの予防に効果があったと言えるか,有意水準1%で検定せよ.
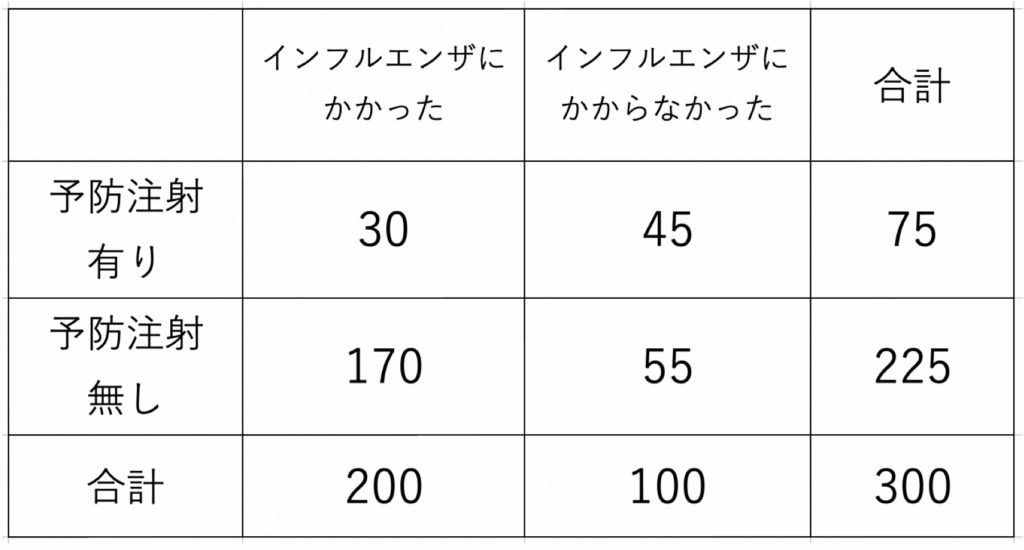
(解)帰無仮説$H_0$ は「注射の有無とインフルエンザにかかるかどうかが独立(関連がない)」となる.この仮定のもとで,期待度数は周辺和を用いて下表のようにまとめられる.
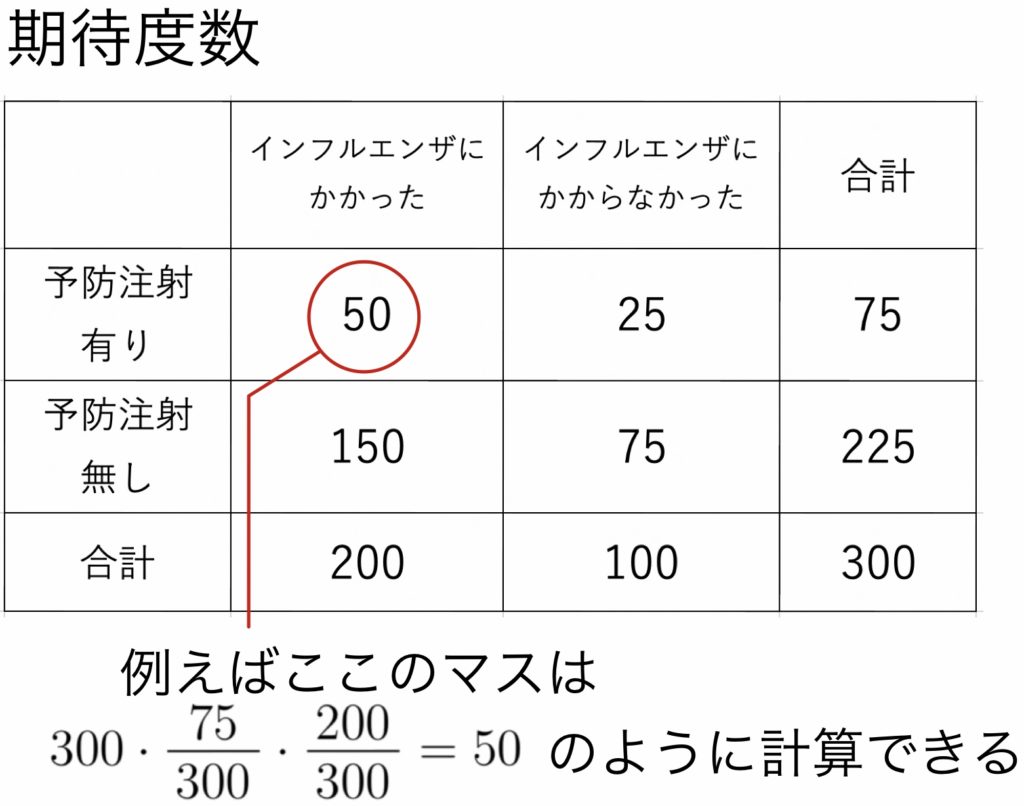
(観測値 – 期待度数)²/(期待度数)の和は自由度1の$\chi^2$ 分布に従う.今回の棄却域は\( \displaystyle \chi^2 (1)\ \ \chi^2>\chi^2_{0.01}(1)=6.63 \)である.
実現値を計算すると,
\(\hspace{2mm}\rule[-1mm]{0mm}{7.5mm} \displaystyle \chi^2=\frac{(30-50)^2}{50}+\frac{(45-25)^2}{25}\)
\(\hspace{10mm}\rule[-1mm]{0mm}{7.5mm} \displaystyle +\frac{(170-150)^2}{150}+\frac{(55-75)^2}{75}=32 \)
よって棄却域に入る ($32>6.63$) から,帰無仮説$H_0$は棄却される.すなわち,インフルエンザの予防に予防注射は効果があったと結論する.
この記事の動画解説版はこちら↓
| 前の記事へ戻る 49 適合度検定 |
次の記事へ 統計量のフローチャート |
| 記事一覧へ戻る 統計学の基礎シリーズ 目次 |
|

