p値

この記事の動画解説版はこちら→統計チャンネル

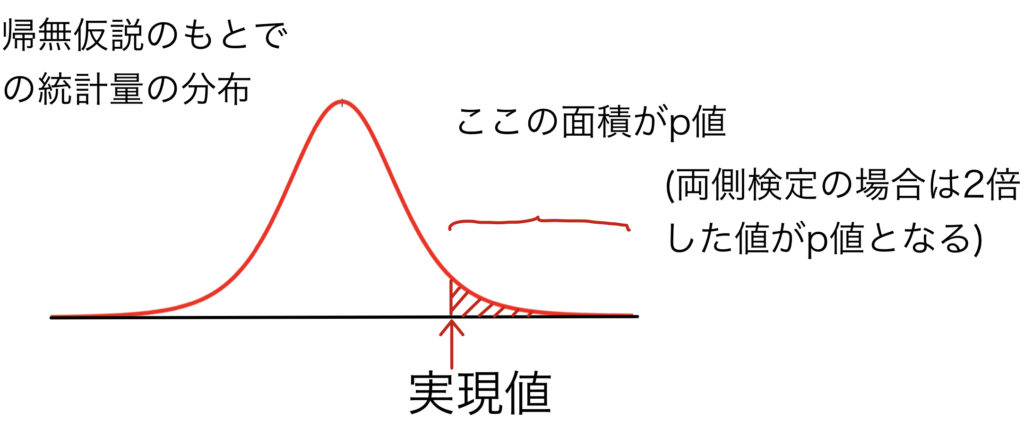
帰無仮説のもとで，検定統計量が実現値以上に極端な値をとる確率を$p$値という．$p$値が有意水準$\alpha$以下の場合は帰無仮説は棄却されることになる．

例えば$p$値が$p=0.03(<0.05)$なら有意水準$5\%$で棄却される．

１円盤

問

機械Aが製造する円盤の直径は正規分布に従うことが知られている．この機械が作る円盤について $10$ 個を無作為に選ぶと，標本平均 $10.3$ cmであった．なお，母分散は$\sigma^2=0.5^2$ であることが経験的に分かっているものとする．
(1) 母平均$\mu$について帰無仮説$H_0: \mu=10$，対立仮説$H_1 : \mu>10$としたときの$p$値として最も適当なものを選択肢の中から選べ．
(2) 母平均$\mu$について帰無仮説$H_0: \mu=10$，対立仮説$H_1 : \mu\not=10$としたときの$p$値として最も適当なものを選択肢の中から選べ．
【選択肢】① $0.023$　② $0.029$　③ $0.047$　④ $0.059$　⑤ $0.10$

解答はこちら
解

(1)使用する統計量は
\(\hspace{2mm}\rule[-1mm]{0mm}{7.5mm} \displaystyle Z=\frac{\overline{X}-\mu}{\sqrt{\sigma^2/n}}\sim\mbox{N}(0,1)\)
実現値は
\(\hspace{2mm}\rule[-1mm]{0mm}{7.5mm} \displaystyle z=\frac{10.3-10}{\sqrt{0.5^2/10}}=1.89\cdots \)
標準正規分布の数値表により，$ P(Z\geqq 1.89)=0.0294$ よって$p$ 値としては②が適する．
(2) 両側検定なので，(1) の値を $2$ 倍して$0.294\times 2 =0.588$．よって④が適する．

本ブログ・解説動画に対応した資料です(note)

この記事の動画解説版はこちら↓

前の記事へ戻る
47 第一種、第二種の誤り,検出力		 次の記事へ
49 適合度検定
記事一覧へ戻る
統計学の基礎シリーズ 目次