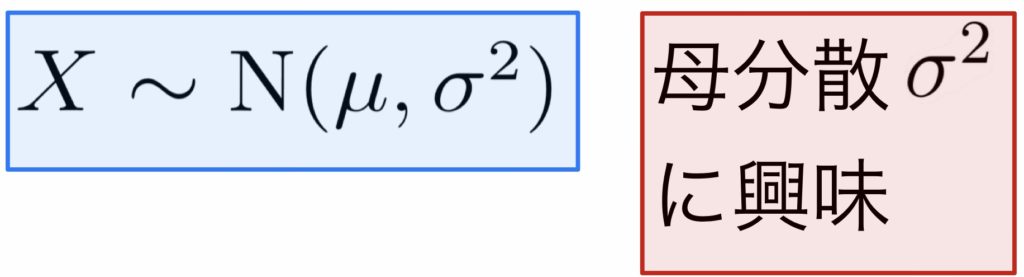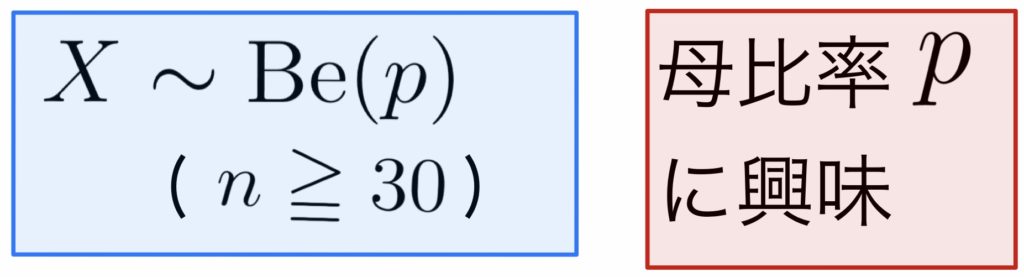よく使う区間推定一覧(1標本)

この記事の動画解説版はこちら→統計チャンネル

よく使う区間推定の手法(1標本)をまとめる．信頼区間の形は母集団分布と興味のある母数の組み合わせから計算できる．なお，この表では信頼係数$1-\alpha$とする(記事42でも同様)．

母集団分布と，興味のある母数

 

 ※ $ X\sim \mbox{?}(\mu, \sigma^2), n\geqq 30$は母集団分布が不明で標本サイズ$30$以上であることを意味する．この状況では中心極限定理により，近似として本表内の統計量を用いる(記事42,44,45でも同様)

対応する統計量と信頼区間はこちら

$\sigma^2$が既知のとき
\( \displaystyle \rule[-1mm]{0mm}{7.5mm}Z=\frac{\overline{X}-\mu}{\sqrt{\sigma^2/n}}\sim \mbox{N}(0,1) \)

信頼区間は
\( \displaystyle \rule[-1mm]{0mm}{7.5mm}\overline{x}\!-\!z_{\alpha/2}\!\cdot\! \sqrt{\frac{\sigma^2}{n}}\leqq \mu \leqq \overline{x}\!+\! z_{\alpha/2}\!\cdot\! \sqrt{\frac{\sigma^2}{n}}\)

$\sigma^2$が未知のとき
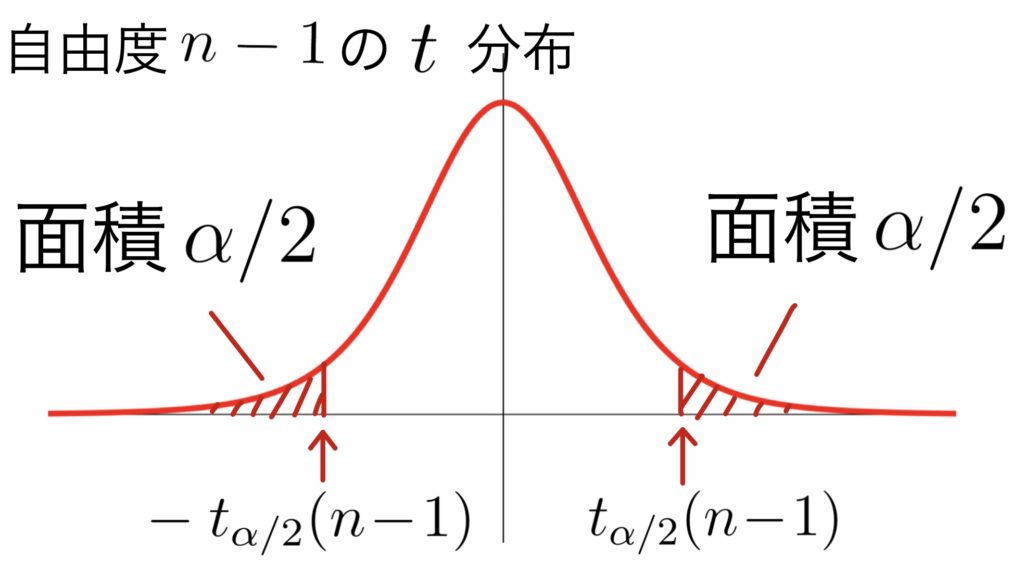
\( \displaystyle \rule[-1mm]{0mm}{7.5mm}T=\frac{\overline{X}-\mu}{\sqrt{U^2/n}}\sim t(n-1) \)

信頼区間は
\( \displaystyle \rule[-1mm]{0mm}{7.5mm}\overline{x}\!-\! t_{\alpha/2}(n\!-\!1)\!\cdot\! \sqrt{\frac{U^2}{n}}\leqq \mu \leqq \overline{x}\!+\! t_{\alpha/2}(n\!-\!1)\!\cdot\!\sqrt{\frac{U^2}{n}}\)
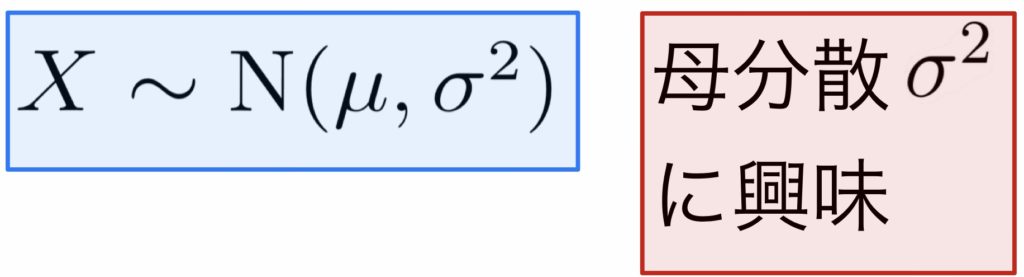
対応する統計量と信頼区間はこちら

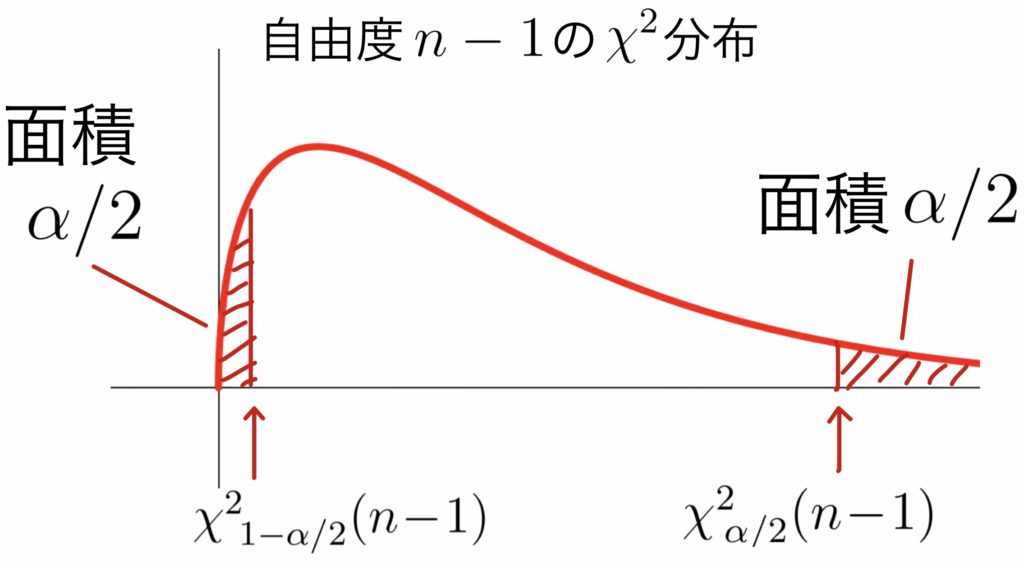
\( \displaystyle \rule[-1mm]{0mm}{7.5mm} \chi^2=\frac{(n-1)U^2}{\sigma^2}\sim \chi^2(n-1) \)
$\rule[-1mm]{0mm}{7.5mm}$信頼区間は
\( \displaystyle \rule[-1mm]{0mm}{7.5mm} \frac{(n-1)\!\cdot\!u^2}{{\chi^2}_{\!\!\alpha/2}(n-1)}\leqq\sigma^2\leqq \frac{(n-1)\!\cdot\!u^2}{{\chi^2}_{\!\!1-\alpha/2}(n-1)}\)

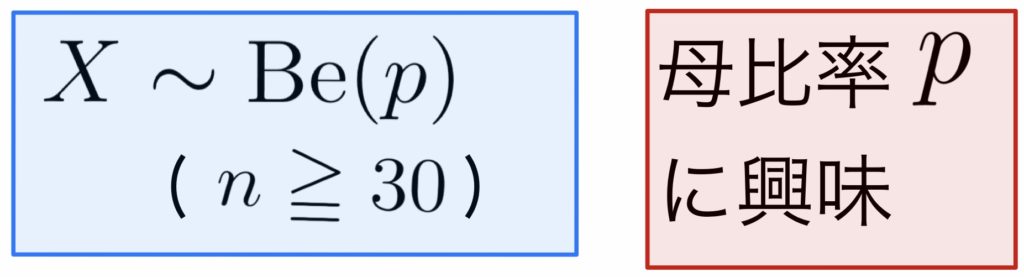
対応する統計量と信頼区間はこちら

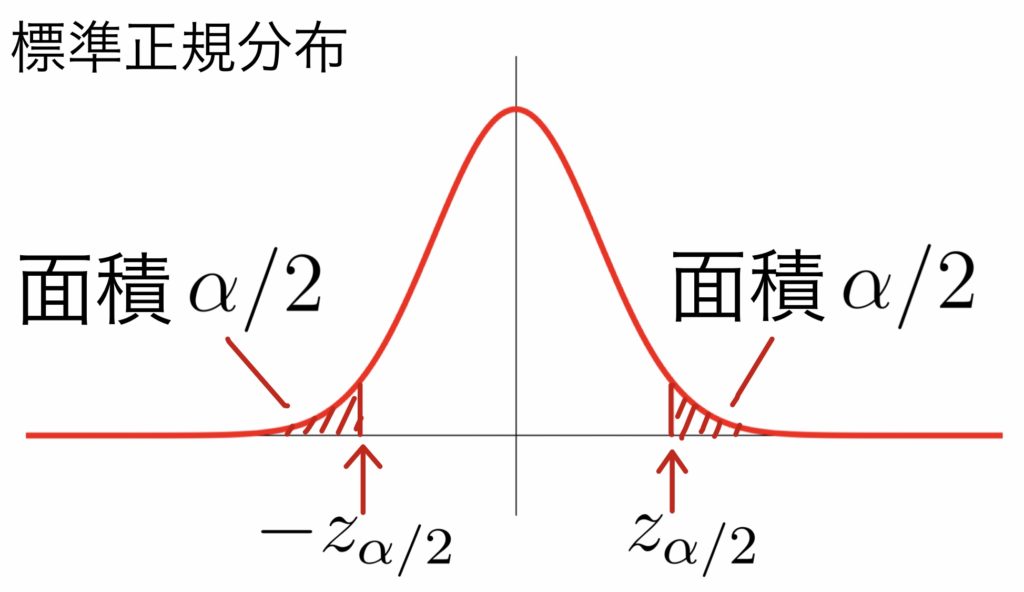
\( \displaystyle \rule[-1mm]{0mm}{7.5mm}Z=\frac{\hat{P}-p}{\sqrt{p(1-p)/n}}\sim\mbox{N}(0,1) \)

信頼区間は
\( \displaystyle \rule[-1mm]{0mm}{7.5mm}\hat{p}-z_{\alpha/2}\!\cdot\!\sqrt{\frac{\hat{p}(1-\hat{p})}{n}}\leqq p \leqq \hat{p}+z_{\alpha/2}\!\cdot\! \sqrt{\frac{\hat{p}(1-\hat{p})}{n}}\)
※根号内の $p$ は推定値 $\hat{p}$ に置き換えている．
問1

平均 $0$ ，分散 $\sigma^2$ の正規母集団から大きさ$20$の標本を抽出して，次の結果を得た．この標本から計算される平均は$1.11$，不偏分散は $8.07$ である．母分散 $\sigma^2$ の$95\%$信頼区間として最も適当なものを選択肢から選べ．

【選択肢】
\( \mbox{①}\, 2.7\leqq\sigma^2\leqq 15.2\ \)
\( \mbox{②}\, 3.7\leqq\mu\leqq 16.2\ \)
\( \mbox{③} \, 4.7\leqq\mu\leqq 17.2 \)

解答はこちら
解

$\displaystyle \frac{19U^2}{\sigma^2}\sim \chi^2(19)$である．

$95\%$信頼区間は
$\displaystyle ({\chi^2}_{\!\!0.975}(19)=)8.91\leqq\frac{19U^2}{\sigma^2}\leqq 32.85(={\chi^2}_{\!\!0.025}(19))$

を$\sigma^2$について解いて
$\rule[-1mm]{0mm}{7.5mm}$ $ \displaystyle \frac{19U^2}{32.85}\leqq \sigma^2\leqq \frac{19U^2}{8.91}$
$\rule[-1mm]{0mm}{7.5mm}$ $U^2=8.07$により$4.66\cdots \leqq \sigma^2\leqq 17.20\cdots $となるから，$\mbox{③}$が適する．

問2

ある政策に関する世論調査で有権者$1000$人中$750$人が賛成と答えた．全有権者のこの政策への賛成率$p$についての$95\%$信頼区間として最も適当なものを選択肢から選べ．
【選択肢】
$\mbox{①}\ 0.729\leqq p \leqq 0.771\ $
$ \mbox{②}\ 0.723\leqq p\leqq 0.777\ $
$ \mbox{③}\ 0.717\leqq p\leqq 0.783$

解答はこちら
解

無作為に選んだ有権者について賛成なら$1$，反対のとき$0$を対応させる確率変数$X_i$は$\displaystyle X_i\sim \mbox{Be}(p)$でこの$p$についての区間推定を行えばよい．中心極限定理により
$\displaystyle \hat{P}=\frac{1}{1000}\sum_{i=1}^{1000}X_i\sim \mbox{N}\left(p,\frac{p(1-p)}{1000}\right)$
$\rule[-1mm]{0mm}{8.5mm}$ 標準化すれば
$\displaystyle \frac{\hat{P}-p}{\sqrt{p(1-p)/1000}}\sim\mbox{N}(0,1)$
$\rule[-1mm]{0mm}{8.5mm}$ $95\%$信頼区間は
$\displaystyle -1.96\leqq \frac{\hat{P}-p}{\sqrt{p(1-p)/1000}}\leqq 1.96$
$\rule[-1mm]{0mm}{8.5mm}$ これを変形して

$\displaystyle \hat{P}-1.96\sqrt{\frac{p(1-p)}{1000}}\leqq p \leqq \hat{P}+1.96\sqrt{\frac{p(1-p)}{1000}}$

ここで$\displaystyle \hat{P}=\frac{750}{1000}=0.75$および区間の両端の$p$を推定値$\displaystyle \hat{p}=0.75$に取り替えて

$\displaystyle 0.75-1.96\sqrt{\frac{0.75(1-0.75)}{1000}}\leqq p \leqq 0.75+1.96\sqrt{\frac{0.75(1-0.75)}{1000}}$

$\rule[-1mm]{0mm}{8.5mm}$ すなわち$0.7231\cdots \leqq p\leqq 0.7768\cdots $で$\mbox{②}$が適する．

本ブログ・解説動画に対応した資料です(note)

この記事の動画解説版はこちら↓

前の記事へ戻る
39 区間推定の一般的な手順		 次の記事へ
41 標本の大きさ問題
記事一覧へ戻る
統計学の基礎シリーズ 目次