大数の法則と中心極限定理

この記事の動画解説版はこちら→統計チャンネル

確率変数の平均 $\displaystyle \overline{X}=\frac{1}{n}\sum_{i=1}^{n}X_i$ を標本平均という．標本平均 $\displaystyle \overline{X}$ について，以下の大数の法則が成り立つことが知られている．

大数の法則

$X_1, X_2, \cdots, X_n$ が互いに独立で，平均 $\mu$ ，分散 $\sigma^2$ の同一の確率分布に従うとする．このとき，任意の $\varepsilon>0$ に対して， $\displaystyle \lim_{n\to\infty}P(|\overline{X}-\mu|<\varepsilon)=1$

この法則により，標本平均 $\displaystyle \overline{X}=\frac{1}{n}\sum_{i=1}^{n}X_i$ は $n$ を大きくするとき，実現値は期待値 $\mu$ に近い値をとることが期待できる．

標本平均 $\displaystyle \overline{X}$ の分布について，以下の中心極限定理が成り立つことが知られている．

中心極限定理

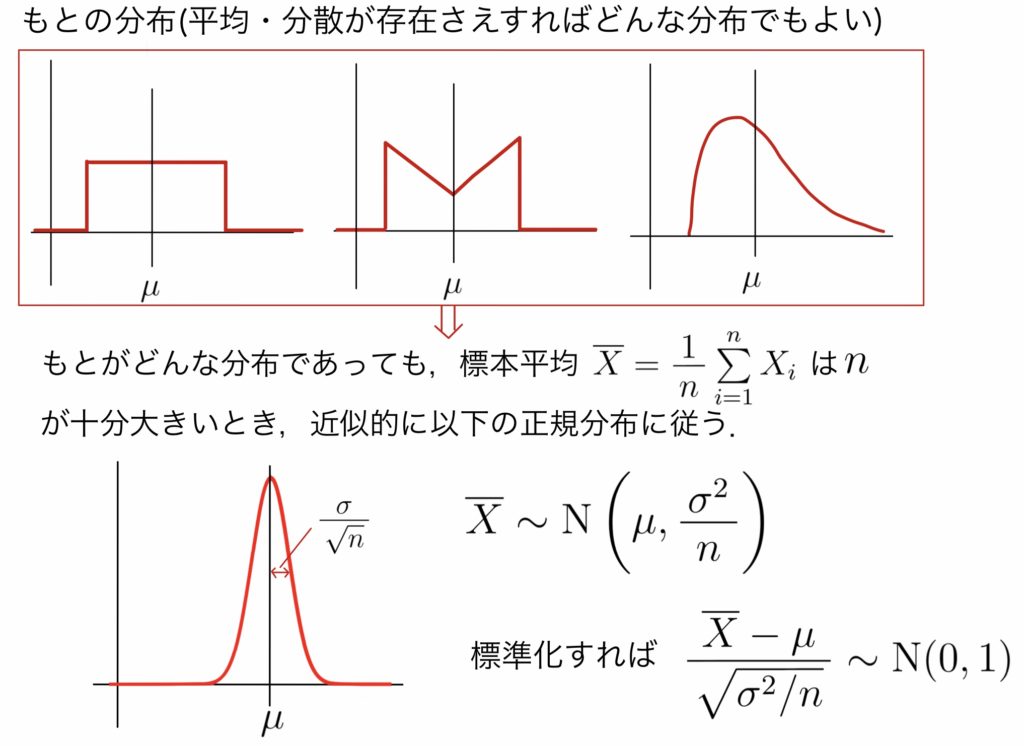
$X_1, X_2, \cdots, X_n$ は互いに独立で，平均 $\mu$ ，分散 $\sigma^2$ の同一の確率分布に従うとする．もとの分布に関わらず，その標本平均 $\displaystyle \overline{X}=\frac{1}{n}\sum_{i=1}^{n}X_i$ は $n$ が大きいとき，近似的に正規分布 $\displaystyle \mbox{N}\left(\mu, \frac{\sigma^2}{n}\right)$ に従う．標準化すれば，近似的に $\displaystyle \frac{\overline{X}-\mu}{\sqrt{\sigma^2/n}}\sim \mbox{N}(0,1)$ 　となる．

中心極限定理を用いて，次の確率を求めてみよう．

(例)サイコロを100個投げるとき，その平均が $4$ 以上となる確率を求めよ．

解

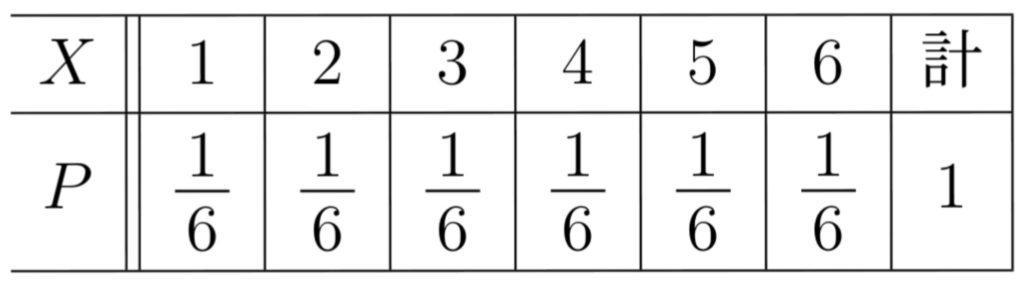
サイコロ1個を投げるときの出る目を $X$ とすると，

$\displaystyle \mu=E(X)=1\cdot \frac16+2\cdot\frac16+\cdots+6\cdot \frac16=\frac72$

$\sigma^2=V(X)=E(X^2)-(E(X))^2$
$\displaystyle \hspace{7mm}=1^2\cdot\frac16+2^2\cdot \frac16+\cdots+6^2\cdot\frac16-\left(\frac72\right)^2$
$\displaystyle \hspace{7mm}=\frac{35}{12}$

(上の計算は記事17,18でも行なっている)

サイコロを100回投げるため，上の分布に従う独立な確率変数 $X_1, X_2, \cdots , X_{100}$ を考える．中心極限定理により，近似的に

　 $\displaystyle \overline{X}=\frac{1}{100}\sum_{i=1}^{100}X_i\sim \mbox{N}\left(\frac72, \frac{35/12}{100}\right)$

標準化して

　 $\displaystyle \frac{\overline{X}-\frac72}{\sqrt{\frac{35/12}{100}}}\sim \mbox{N}(0,1)$

よって求める確率は

　 $\displaystyle P(\overline{X}\geqq 4)$
　　 $=P\left(\frac{\overline{X}-\frac{7}{2}}{\sqrt{\frac{35/12}{100}}}\geqq \frac{4-\frac{7}{2}}{\sqrt{\frac{35/12}{100}}}=2.927\cdots \right)$
　　 $\fallingdotseq 0.0017(0.17\%)$

ただし最後の確率は標準正規分布の上側確率の数値表から求めた．

この範囲のテキスト試読はこちら

本ブログ・解説動画に対応した資料です(note)

この記事の動画解説版はこちら↓

前の記事へ戻る 29 正規分布の標準化	次の記事へ 31 二項分布の正規分布近似
記事一覧へ戻る統計学の基礎シリーズ目次

サイト運営者