正規分布の標準化

この記事の動画解説版はこちら→統計チャンネル

標準正規分布

$X\sim \mbox{N}(\mu, \sigma^2)$のとき，\( \displaystyle  Z=\frac{X-\mu}{\sigma} \)とすれば$Z \sim \mbox{N}(0,1)$となることが知られている(一般に，$X$が正規分布に従うならば，その1次式$aX+b$も正規分布に従うことが知られている)．このことから，一般の正規分布$\mbox{N}(\mu,\sigma^2)$における確率計算は平均が$0$，分散が$1$の正規分布の計算に帰着させることができる．

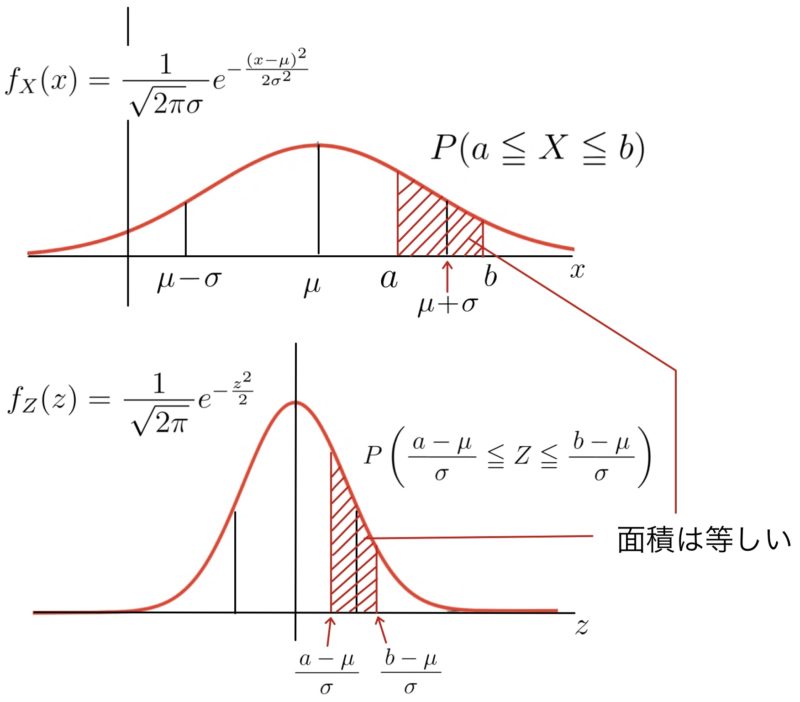
$\mbox{N}(0,1)$は標準正規分布といい，$0.00$から$3.99$まで$0.01$刻みの$\alpha$に対して上側確率($\alpha$以上の値をとる確率)

　\( \displaystyle  z_{\alpha}=P(X\geqq \alpha) \)

について，数表ページにまとめられている(本によっては，$0$から$\alpha$の間の値をとる確率を与える形式の数値表を採用している場合もある)．

正規分布の再生性

正規分布は再生性をもつことが知られている．すなわち，

　$X_1,X_2$が独立のとき，
　$\rule[-1mm]{0mm}{7.5mm} X_1\sim \mbox{N}(\mu_1, {\sigma_1}^2), X_2\sim \mbox{N}(\mu_2, {\sigma_2}^2)$
　$\rule[-1mm]{0mm}{7.5mm}\Rightarrow X_1+X_2\sim \mbox{N}(\mu_1+\mu_2, {\sigma_1}^2+{\sigma_2}^2)$

問

$X\sim \mbox{N}(10, 5^2)$のとき，次の確率を求めよ．

(1) $P(X\geqq 17.5)$
(2) $P(X\leqq 0)$
(3) $P(-3\leqq X\leqq 3)$

解答はこちら
解

$X\sim \mbox{N}(10, 5^2)$により$Z=\frac{X-10}{5}\sim\mbox{N}(0,1)$

(1) $P(X\geqq 17.5)=P\left(\frac{X-10}{5}\geqq \frac{17.5-10}{5}\right)$
$\hspace{10mm}=P(Z\geqq 1.5)=0.0668$

(2) $P(X\leqq 0)=P\left(Z\leqq \frac{0-10}{5}\right)$
$\hspace{10mm}=P(Z\leqq -2)=P(Z\geqq 2)$
$\hspace{10mm}=0.0228$

(3)※スマホでは横スクロールします．

$P(-3\leqq X\leqq 13)=P\left(\frac{-3-10}{5}\leqq Z\leqq \frac{13-10}{5}\right)$
$\hspace{10mm}=P(-2.6\leqq Z\leqq 0.6)$
$\hspace{10mm}=P(Z\geqq -2.6)-P(Z\geqq 0.6)$
$\hspace{10mm}=(1-P(Z\leqq -2.6))-P(Z\geqq 0.6)$
$\hspace{10mm}=(1-P(Z\geqq 2.6))-P(Z\geqq 0.6)$
$\hspace{10mm}=(1-0.0047)-0.2743=0.721$

本ブログ・解説動画に対応した資料です(note)

この記事の動画解説版はこちら↓

前の記事へ戻る
28 正規分布		 次の記事へ
30 大数の法則と中心極限定理
記事一覧へ戻る
統計学の基礎シリーズ 目次