正規分布

この記事の動画解説版はこちら→統計チャンネル

確率密度関数が以下で与えられる分布を正規分布といい，$\mbox{N}(\mu, \sigma^2)$と表す．ただし，$e=2.71828\cdots$はネイピア数である．

　$\displaystyle f(x)=\frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{(x-\mu)^2}{2\sigma^2}}$
　　($\mu$は定数，$\sigma$は正の定数)

$X\sim \mbox{N}(\mu, \sigma^2)$のとき，$E(X)=\mu, V(X)=\sigma^2$となる．

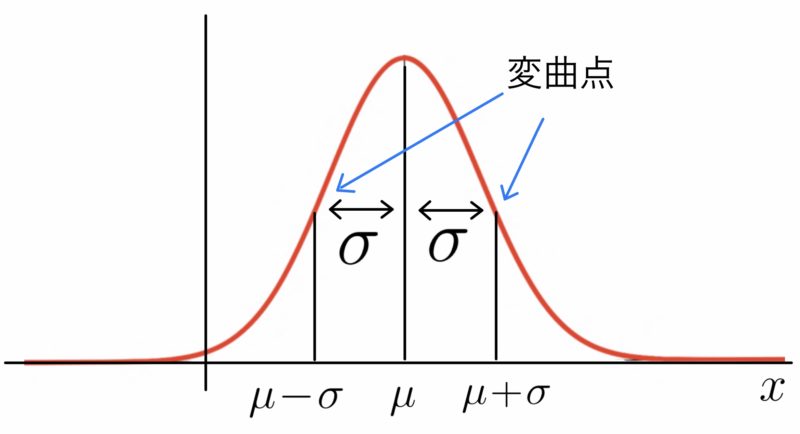
正規分布の特徴として，以下の(1)-(3)が挙げられる．

(1) 直線$x=\mu$を中心に左右対称
(2) $x=\mu\pm \sigma$が変曲点(凹凸が変わる)
(3) $\sigma$が大きくなると下につぶれる(横に広がる)

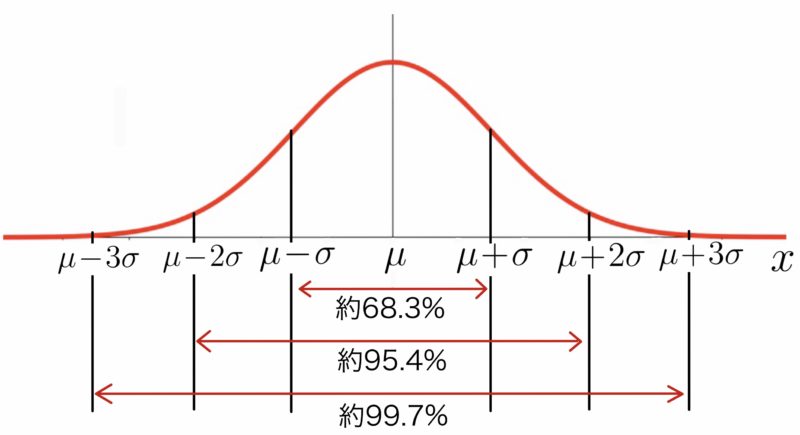
正規分布において，$\mu$から$\pm \sigma$，$\pm 2\sigma$，$\pm 3\sigma$の範囲の確率はそれぞれ次のようになる．これらの結果は今後よく使うので覚えておくとよい．

　$P(\,\mu-\, \sigma\leqq X\leqq \,\mu+\, \sigma)\, \fallingdotseq 0.683$
　$P(\mu-2\sigma\leqq X\leqq \mu+2\sigma)\fallingdotseq 0.954$
　$P(\mu-3\sigma\leqq X\leqq \mu+3\sigma)\fallingdotseq 0.997$

問

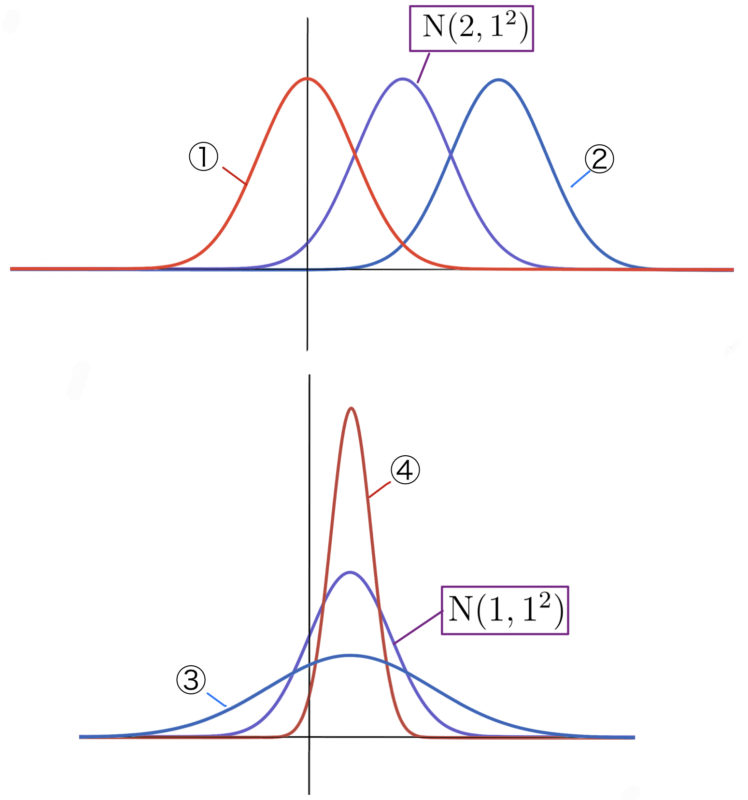
次のグラフ①〜④のうち，$\mbox{N}(1,0.5^2)$の分布を表すものとして最も適切なものを1つ選べ．

本ブログ・解説動画に対応した資料です(note)

この記事の動画解説版はこちら↓