この記事の動画解説版はこちら→統計チャンネル
ポアソン分布
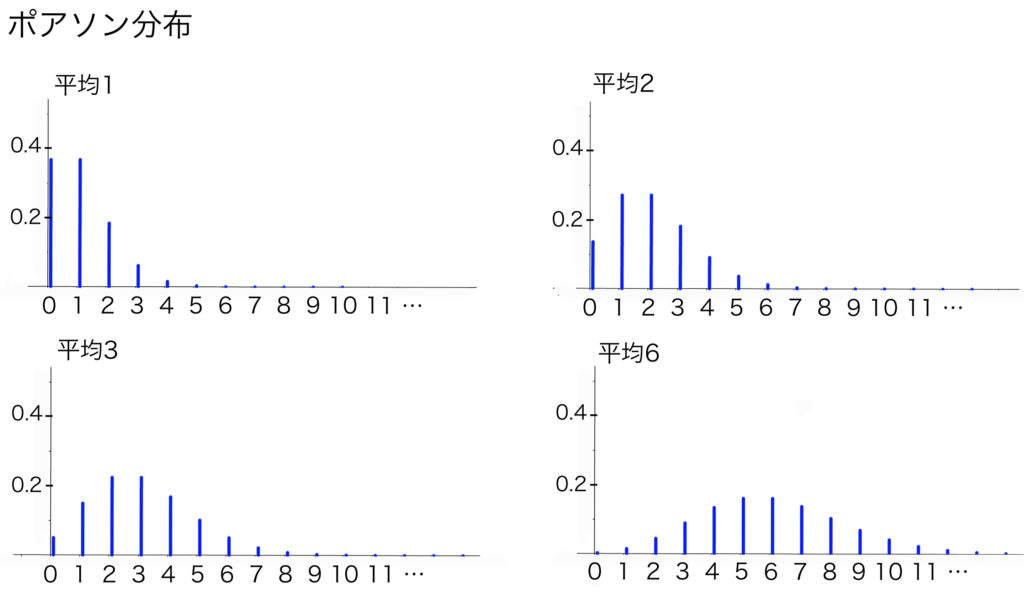
二項分布において,平均を固定した上で,成功確率を小さくした(極限の)分布としてポアソン分布とよばれる分布が定義できる.
この記事は数学の扱いが多いが,難しいと感じる部分は読み飛ばしても構わない(記事下部の問を解くだけでも構わない).
二項分布において期待値$np=\lambda>0$を固定した上で,成功確率$p$について$p\to 0$(このとき$n\to\infty$となる)と極限をとった確率分布としてポアソン分布(Poisson distribution)$\mbox{Po}(\lambda)$が定義される.
$ \displaystyle P(X=k)=e^{-\lambda}\frac{\lambda^k}{k!}\ \ (k=1,2,3,\cdots)$
ここで,$e$はネイピア数$e=2.71828\cdots$を表す.

二項分布からポアソン分布が導かれる計算は次の通り(※スマホでは横スクロールします).
$p\to 0$のとき,$n\to\infty$である.
$\displaystyle = \frac{(n-0)(n-1)\cdots (n-(k-1))}{k(k-1)\cdots 2\cdot 1}p^{k}(1-p)^{n-k}$
$\displaystyle = \frac{1}{k!}\cdot \left(1- \frac{0}{n}\right)\left(1- \frac{1}{n}\right)\left(1- \frac{2}{n}\right)\cdots \left(1- \frac{k-1}{n}\right)\cdot (np)^k \frac{(1-p)^n}{(1-p)^k}\cdots (\mbox{☆})$
ここで$\displaystyle np=\lambda, (1-p)^n=\left(1- \frac{\lambda}{n}\right)^n\to e^{-\lambda} (n\to\infty)$などにより $\mbox{☆}$は$p\to 0 $のとき$\displaystyle \frac{1}{k!}\lambda^ke^{-\lambda}$となる.
ポアソン分布の式
$ \displaystyle P(X=k)=e^{-\lambda}\frac{\lambda^k}{k!}\ (k=1,2,3,\cdots)$
は,以下の指数関数の級数表示を知っていると思い出しやすい.
$ \displaystyle e^{\lambda}=\sum_{k=0}^{\infty}\frac{\lambda^k}{k!}$
$ \displaystyle =\frac{\lambda^0}{0!}+\frac{\lambda^1}{1!}+\frac{\lambda^2}{2!}+\cdots$
すなわち級数表示の各項にそれぞれ$e^{-\lambda}$をかけたものがポアソン分布の$X=0,1,2,\cdots $での確率である.$X=0,1,2,\cdots $での確率の合計が$1$となることは,この級数表示から分かる.
導出過程からもわかるように,試行回数$n$が大きく成功確率$p$が小さい二項分布はポアソン分布で近似できる(現実の問題では,$n>50$かつ$np\leqq 5$を目安にできる.村上・安田著『統計学演習』).
ポアソン分布は,時間や空間に関して分布しているような現象で用いられることが多い.例えば,1時間に電話がかかってくる回数,ある都市における1日の交通事故件数,砂漠地域で1単位面積で発見される隕石の数,1枚の金属板のきずの数などはポアソン分布がよく当てはまる例として知られている.例えば1時間に電話がかかってくる回数$X$については,次のようにしてポアソン分布に従うことがわかる.過去のデータから平均が$\lambda>0$とわかっているものとする.1時間を$n$等分して$1/n$時間の間に電話がかかる回数$X_i$は,$n$が十分大きければ成功確率$\lambda/n$のベルヌーイ分布で近似できると考えられる(分割$n$が大きいため,$1/n$時間の間に2回以上電話がかかる可能性は無視できるものとしてよい).ここで$n$個の小時間ごとのベルヌーイ分布$X_1,X_2,\cdots, X_n$が独立であるとすれば,$ \displaystyle X=\sum_{i=1}^{n}X_i$と表されることから$X$は$\mbox{B}(n,\lambda/n)$に従う(前回扱ったように,ベルヌーイ分布の和は二項分布となる).この二項分布は平均$np=n\cdot \lambda/n=\lambda$が一定で成功確率が小さい(また,試行回数$n$は大きい)分布であるから,ポアソン分布で近似できることになる.
ポアソン分布の期待値と分散は次のようになる.
$\displaystyle E(X)=\lambda,\ V(X)=\lambda$
この結果は,二項分布$\mbox{B}(n,p)$の期待値$np$,分散$np(1-p)$において$np=\lambda$と固定して$p\to 0$としたものとして理解できる.
二項分布・ポアソン分布の再生性
成功確率が等しく独立に二項分布に従う確率変数の和は再び二項分布になる.これを再生性という.同様に、ポアソン分布も再生性をもつ.式でかけば,以下の通り.
$X_1, X_2$が独立であるとする.
(1) $\rule[-1mm]{0mm}{7.5mm} X_1\sim \mbox{B}(n_1, p), X_2\sim \mbox{B}(n_2, p)$
$\Rightarrow X_1+X_2\sim \mbox{B}(n_1+n_2, p)$
(2) $\rule[-1mm]{0mm}{7.5mm} X_1\sim \mbox{Po}(\lambda_1), X_2\sim \mbox{Po}(\lambda_2)$
$\Rightarrow X_1+X_2\sim \mbox{Po}(\lambda_1+\lambda_2)$
実際,二項分布はベルヌーイ分布の和として表されるから,成功確率$p$の「二項分布と二項分布の和」は成功確率$p$のベルヌーイ分布の和となり,(1)が成り立つ.また,厳密には証明が必要であるが,ポアソン分布は二項分布で極限をとって計算された分布であるから,二項分布の再生性が遺伝して(2)も成り立つ.
ある都市における1日当たりの交通事故における死者の数$X$は,平均$0.9$人のポアソン分布に従うという.このとき次の確率を求めよ.なお,必要であれば$e^{0.9}\fallingdotseq2.46$を用い,答えは小数第4位を四捨五入せよ.
(1) $P(X=0)$ (2) $P(X>2)$
この記事の動画解説版はこちら↓
| 前の記事へ戻る 23 二項分布 |
次の記事へ 25 幾何分布 |
| 記事一覧へ戻る 統計学の基礎シリーズ 目次 |
|

