この記事の動画解説版はこちら→統計チャンネル
二項分布
成功確率$p$のベルヌーイ試行を$n$回繰り返したときの成功回数$X$の分布を二項分布(Binomial Distribution)といい,$\mbox{B}(n,p)$と表す.$p=0,2. 0.4, 0.6$での分布を示す.

$X\sim \mbox{B}(n,p)$のとき確率分布は式で
$ \displaystyle P(X=k)={}_nC_k \, p^kq^{n-k}$…①
のように表される(ただし$q$は$q=1-p$(失敗確率)).これは以下のような例で考えると納得しやすい.
(例)さいころを5回投げるときに$5$以上の目がでる回数を$X$とする.1回投げるときの$5$以上の目がでる確率は\( \displaystyle \frac26=\frac13 \)であるから,$X$は試行回数$5$,成功確率$ \displaystyle p=\frac13$ の二項分布に従う.$X=0,1,2$の確率をそれぞれ求めてみよう.
$X=0$は5回ともすべて失敗する場合であるから,$\displaystyle q^5=\left(\frac23\right)$,すなわち
\( \displaystyle P(X=0)=\left(\frac23\right)^5 \)
と表される(以下図では成功を○,失敗を×で表すことにする).
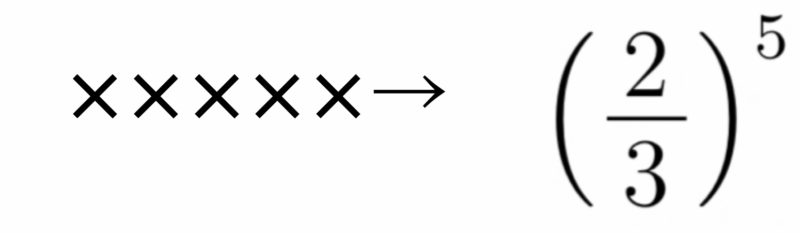
$X=1$は5回のうち1回だけ成功し,残り4回は失敗する場合である.これは○××××,×○×××,××○××,×××○×,××××○の5通りの場合があり,それぞれ確率が\( \displaystyle pq^4=\left(\frac13\right)\cdot\left(\frac23\right)^4 \)であるから,
\(\displaystyle P(X=1) = 5\cdot\left(\frac13\right)\!\cdot\! \left(\frac23\right)^4\)

$X=2$は5回のうち2回だけ成功し,残り3回は失敗する場合である.これは○○×××,○×○××,○××○×,…など$5$箇所から$2$箇所選ぶ$ \displaystyle {}_5C_2=\frac{5\cdot 4}{2\cdot 1}=10$ 通りの場合があり,それぞれ確率が\( \displaystyle p^2q^3=\left(\frac13\right)^2\cdot\left(\frac23\right)^3 \)であるから,
\( \displaystyle P(X=2)={}_5C_2\cdot\left(\frac13\right)^2\!\cdot\! \left(\frac23\right)^3\)

以上の考察により,成功回数$k$となる確率は次の式で表されることが分かる.
$ \displaystyle P(X=k)={}_5C_k \left(\frac13\right)^k\!\cdot\! \left(\frac23\right)^{n-k}$
上の最終式で試行回数$n$,成功確率$p$,失敗確率$q(=1-p)$に置き換えて一般化したものが①である.
二項分布の平均と分散
$X\sim \mbox{B}(n,p)$とする.二項分布は互いに独立にベルヌーイ分布$\mbox{Be}(p)$に従う確率変数$X_1,X_2,\cdots , X_n$の和として
$X=X_1+X_2+\cdots +X_n$
のように表される.よって二項分布の期待値と分散は以下のようになる.
$E(X)=np, V(X)=npq$
ある試験は問題が全部で10問あり,各問題は○か×の2つの選択肢からなる.
ある受験生が各問題ごとにランダムに解答するとき,その正答数を$X$とする.
(1) $X$は二項分布$\mbox{B}(n,p)$に従う.$n,p$の値はなにか.
(2) $P(X\leqq 2)$を求めよ.
(3) $E(X), V(X)$を求めよ.
この記事の動画解説版はこちら↓
| 前の記事へ戻る 22 ベルヌーイ分布 |
次の記事へ 24 ポアソン分布 |
| 記事一覧へ戻る 統計学の基礎シリーズ 目次 |
|

