この記事の動画解説版はこちら→統計チャンネル
もくじ
同時分布
2つの確率変数$X,Y$のとりうる値とその確率との対応関係を$X,Y$の同時確率分布という．
$P(X=x_i, Y=y_j)=p_{ij}$
$(i=1,2,\cdots, j=1,2,\cdots )$
を同時確率関数という．同時確率関数を用いれば，同時確率分布は下図のように表される．
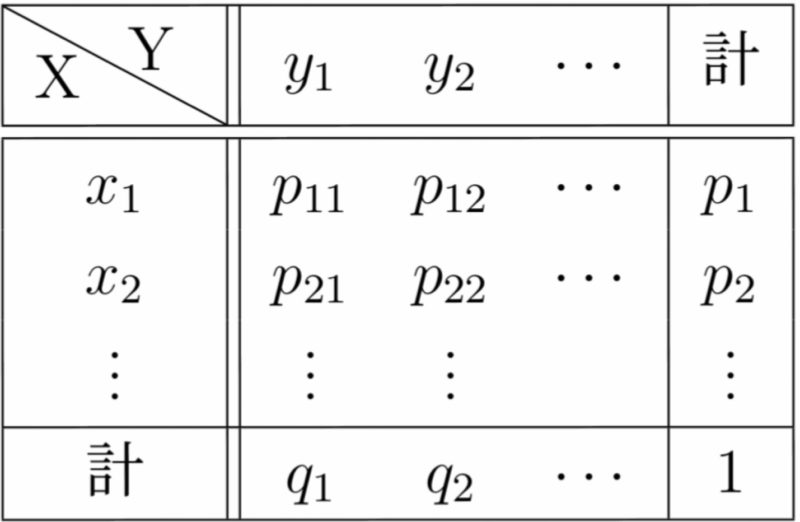
また，
$\displaystyle P(X=x_i)=\sum_{j}p_{ij}=p_i\ (i=1,2,\cdots)$
$\displaystyle P(Y=y_j)=\sum_{i}p_{ij}=q_j\ (j=1,2,\cdots)$
をそれぞれ$X,Y$の周辺確率関数といい，その分布を周辺分布という．
確率変数の独立性
確率変数$X$のとる値が確率変数$Y$の確率に影響を与えないとき，すなわち
すべての$j=1,2,\cdots$で
\( \displaystyle\begin{eqnarray} P(Y=y_j) &=&P(Y=y_j|X=x_1)\\ &=&P(Y=y_j|X=x_2)\\ &=&\cdots \end{eqnarray}\)
となるとき，$X,Y$は独立(あるいは互いに独立)であるという．
(補足) 上の独立性の定義は次のようにも言い換えられる．
すべての$i,j$で
$P(X=x_i, Y=y_j)=P(X=x_i)P(Y=y_j)$
(言い換えると「すべての$i,j$で$p_{ij}=p_iq_j$」，すなわち同時確率関数が周辺確率関数の積で表されることである．)
3つの確率変数$X, Y, Z$に対しても，その独立性が以下のように定義される(3つ以上でも同様)．
すべての$i, j, k $ で
$ \displaystyle P(X=x_i, Y=y_j,Z=z_k)$
$\displaystyle =P(X=x_i)P(Y=y_j)P(Z=z_k)$
(補足2) 記事26で扱う連続型の確率変数に対しても，独立性の概念が上補足と同様な形で定義される．すなわち，$X,Y$の同時確率密度関数$f(x,y)$と周辺分布$f_X(x), f_Y(y)$に対して
すべての$x,y$で $f(x,y)=f_X(x)f_Y(y)$
が成り立つとき，$X,Y$は独立であるという．
確率変数の和と積の期待値
確率変数の和$X+Y$や積$XY$の期待値について，次のことがいえる．
(1) $E(X+Y)=E(X)+E(Y)$
(2) $X,Y$が独立のとき，
$E(XY)=E(X)E(Y)$
(逆に，この式が成り立っていても$X,Y$が独立であるとは限らない)
(証明)(1)同時確率関数を$P(X=x_i, Y=y_j)=p_{ij}$とおく．
\( \displaystyle\begin{eqnarray} E(X+Y) &=&\sum_{i}\sum_{j}(x_i+y_j)p_{ij}\\ &=&\sum_{i}\sum_{j}x_ip_{ij}+\sum_{i}\sum_{j}y_jp_{ij} \\ &=&\sum_{i}x_i\sum_{j}p_{ij}+\sum_{j}y_j\sum_{i}p_{ij}\\ &=&\sum_{i}x_ip_i+\sum_{j}y_jq_j\\ &=&E(X)+E(Y)\end{eqnarray}\)
(2)$X,Y$が独立のとき，すべての$i,j$で$p_{ij}=p_iq_j$であるから
\( \displaystyle\begin{eqnarray} E(XY) &=&\sum_{i}\sum_{j}x_iy_jp_{ij}\\ &=&\sum_{i}\sum_{j}x_{i}y_jp_iq_j \\ &=&\sum_{i}x_ip_i\sum_{j}y_jq_j \\ &=&\sum_{i}x_ip_i E(Y)\\ &=&E(Y)\sum_{i}x_ip_i\\ &=&E(Y)E(X)\end{eqnarray}\)
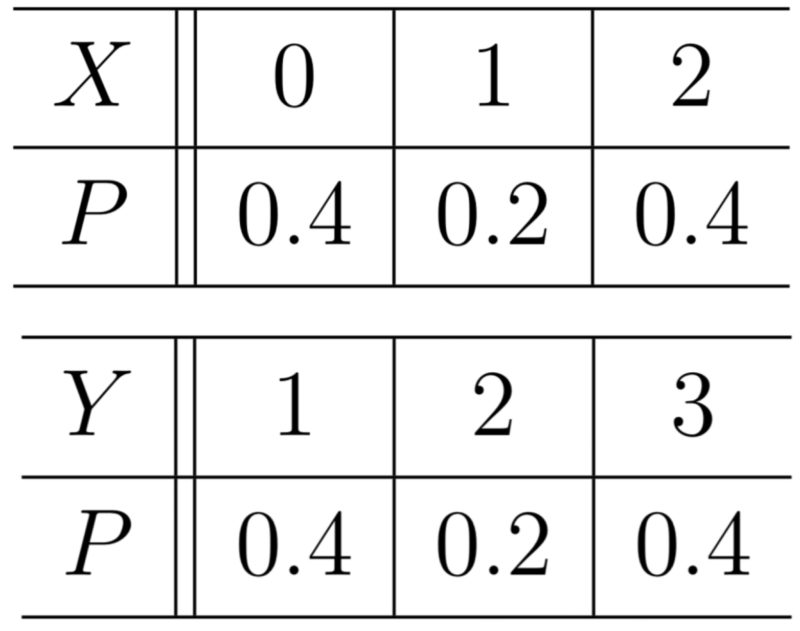
次の表は確率変数$X,Y$の同時分布である．
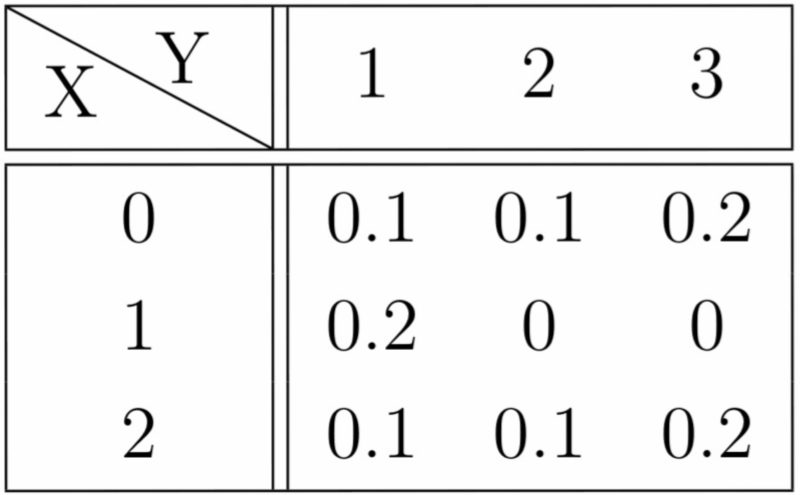
(1) $X,Y$の周辺分布を求めよ．
(2) $E(X), E(Y), E(XY)$を求めよ．
(3) $X,Y$は独立ではないことを示せ．
(1) $X,Y$の周辺分布は，同時分布において行ごと・列ごとに確率を合計すればよい．
(2) $E(X)=0\cdot 0.4+1\cdot 0.2+2\cdot0.4=1$
$E(Y)=1\cdot 0.4+2\cdot 0.2+3\cdot0.4=2$
$E(XY)=0\!\cdot\! 1\times0.1+0\!\cdot \!2\times 0.1+0\cdot\! 3\times 0.2$
$+1\!\cdot\! 1\times 0.2+1\!\cdot\! 2\times \ 0 +1\!\cdot\! 3\times 0$
$+2\!\cdot\! 1\times 0.1+2\!\cdot\! 2\times \ 0.1 +2\!\cdot\! 3\times 0.2=2$
(今回の例では$Y=X+1$となっているので，$E(Y)=E(X+1)=E(X)+1$ $=1+1=2$とも求められる．)
(3) $0.1=P(X=0,Y=1)$
$\hspace{15mm}\not=P(X=0)P(Y=1)=0.4\cdot 0.4$
により$X,Y$は独立ではない．
(補足: この問題は$E(XY)=E(X)E(Y)$だが$X,Y$が独立ではない例となっている)
本ブログ・解説動画に対応した資料です(note)
この記事の動画解説版はこちら↓
| 前の記事へ戻る 19 確率変数の標準化 |
次の記事へ 21 確率変数の和の期待値と分散 |
| 記事一覧へ戻る 統計学の基礎シリーズ 目次 |
|