この記事の動画解説版はこちら→統計チャンネル
1つのモノ(人)を選ぶ条件付き確率において，問題設定を1枚の正方形に整理すると解きやすい場合がある．
(例)集団Aは5%の人が病気にかかっている．病気Xを診断する検査で，病気Xにかかっている人が正しく陽性と判断される確率は80%，病気Xにかかっていない人が誤って陽性と判断される確率は10%であるとする．すなわち
とする．集団Aのある人がこの検査を受けたとき，次の確率を求めよ．
(1) その人が陽性と判定される確率
(2) 陽性と判定されたとき，その人が病気Xにかかっている確率
(解)
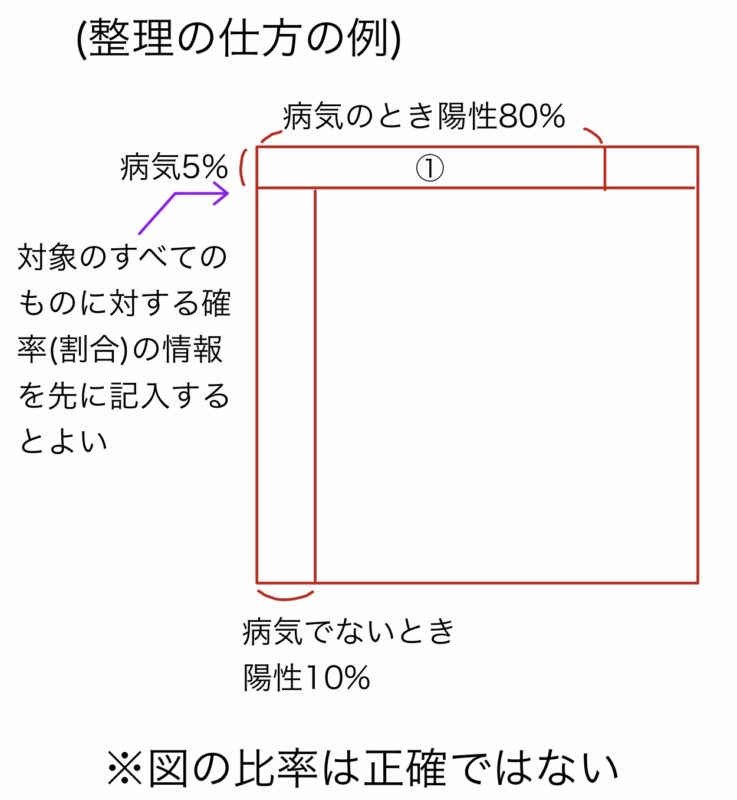
(1)正方形の1辺を1とし，L字部分の面積を求めればよい．
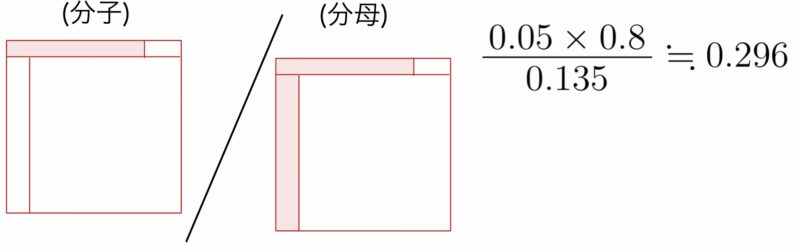
(2) L字部分の面積に占める①の面積割合を求めればよい．
問
製品Xを工場A，Bで製造しているが，それぞれ3%，4%の割合で不良品が発生するものとする．ある電気店は製品Xについて，工場Aから80%，工場Bから20%の割合で仕入れをしている．
(1) 電気店に仕入れされた製品Xをランダムに1つ選ぶとき，これが工場Bから製造された不良品である確率を求めよ．
(2) 電気店に仕入れされた製品Xをランダムに1つ選んだところ，不良品であった．このとき，この製品が工場Bで製造されたものである確率を求めよ．
解答はこちら
解
(1)上図で1辺を1として②の面積を求めればよい．
$$0.2\times0.04=0.008$$
(2) 上図で(①と②の面積)に対する②の面積の割合を求めればよい．
$$ \frac{0.2\times 0.04}{0.8\times0.03+0.2\times 0.04}= \frac{0.008}{0.032}=0.25$$
本ブログ・解説動画に対応した資料です(note)
この記事の動画解説版はこちら↓
| 前の記事へ戻る 15 条件付き確率 |
次の記事へ 17 確率変数 |
| 記事一覧へ戻る 統計学の基礎シリーズ 目次 |
|