コレログラム

この記事の動画解説版はこちら→統計チャンネル

時系列データ$\{y_t|t=1,,2,\cdots T\}$と，もとの時系列データと$h$地点だけずらした(ラグをつけた)データ$\{y_{t+h}|h=1,2,\cdots, T-h\}$について，以下の式で定義される自己相関係数$r_h$によってその相関を調べることができる．

$$C_h=\frac{1}{T}\sum_{t=1}^{T-h}(y_t-\overline{y})(y_{t+h}-\overline{y}), r_h=\frac{C_h}{C_0}$$

自己相関係数$r_0, r_1, r_2, \cdots$を並べたグラフをコレログラムといい，データの周期性を調べるのに役立つ．

コレログラムの例を示す．

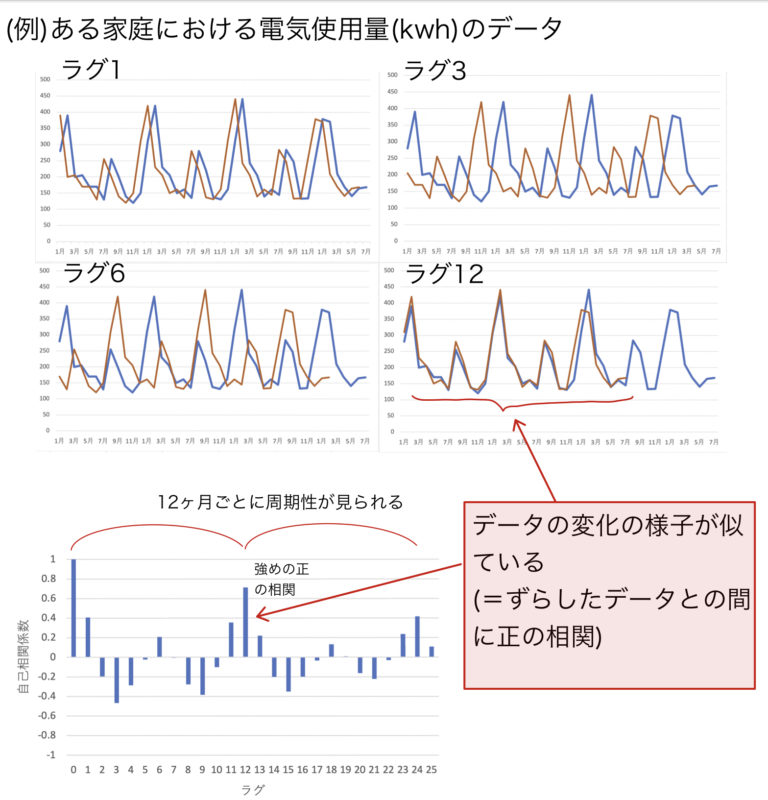
上記の電気使用量の例では，12ラグ(12ヶ月)ずらしたグラフがもとのグラフと似た変化をすることが，コレログラムにおいてラグ12の値が大きくなっていることに対応している．

問

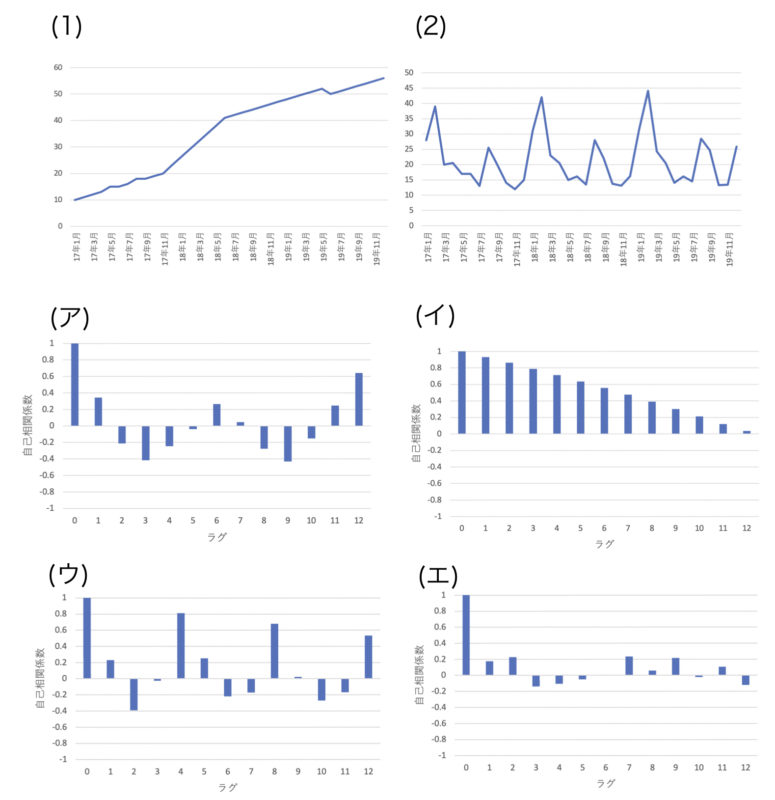
次の(1)，(2)はそれぞれ月ごとにある値を観測したデータのグラフである．これらに対応するコレログラムとして最も適当なものを(ア)〜(エ)の中から選べ．

この範囲のテキスト試読はこちら

本ブログ・解説動画に対応した資料です(note)

この記事の動画解説版はこちら↓