変動分析

この記事の動画解説版はこちら→統計チャンネル

変動分析

経済に関する時系列データは，その構成を次のような3種類に分けて考えることが多い．

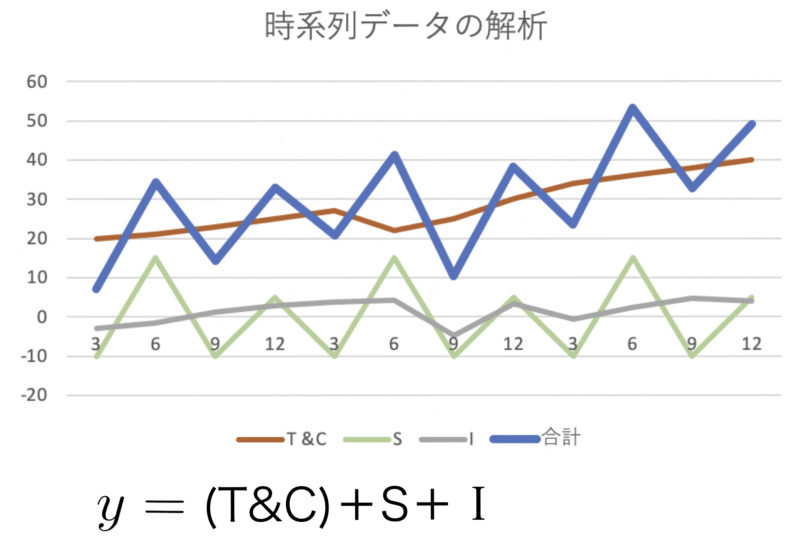
傾向変動(T &C)…比較的長期の傾向で，景気変動なども含む．この傾向変動は単調な長期的傾向(トレンド)とトレンドの周りで上下する周期の定まっていない循環的傾向(サイクル)に分けることもある．

季節変動(S)…季節によって左右される1年を周期として規則的に繰り返される変動．

不規則変動( I )…上記以外の説明がつきにくい突発的な変動や不規則かつ短期間の上下におきる小さい変動．期待値(平均値)を0と仮定する．

移動平均

移動平均は前後のデータを含めた平均であり，周期的な影響を取り除くときなどに用いられる．

以下に1日〜30日までの架空のデータについて，7日間移動平均の例を示す．4日の7日間移動平均は1日〜7日の平均，5日の7日間移動平均は2日〜8日の平均，…のようにその日にちを中心にした前後7日間の平均として移動平均が求められる．

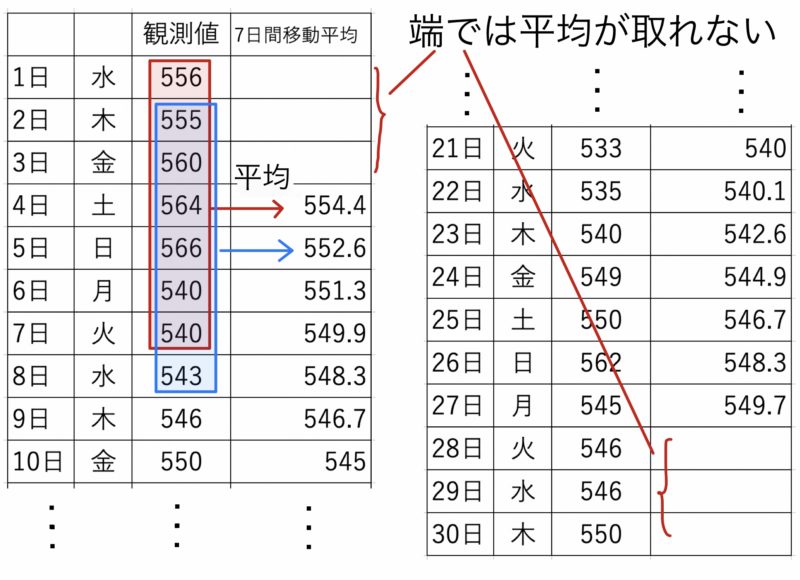
一般に，移動平均のグラフは元のグラフよりも滑らかになる．また，上の例では7日間移動平均は曜日の影響を取り除いた傾向変動を表す．

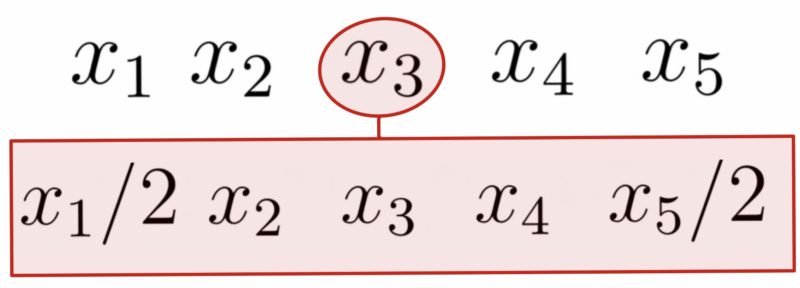
4項移動平均，6項移動平均のように，期間が偶数個の場合の移動平均は，期間を1つ大きくし，両端の値を1/2したものを期間の数でわったものとして計算する(中心化移動平均という)．例えば$x_1, x_2, x_3, x_4, x_5$という時系列データにおいて，$x_3$の4日間移動平均は以下のように計算される．

$$\frac{x_1/2+x_2+x_3+x_4+x_5/2}{4}$$

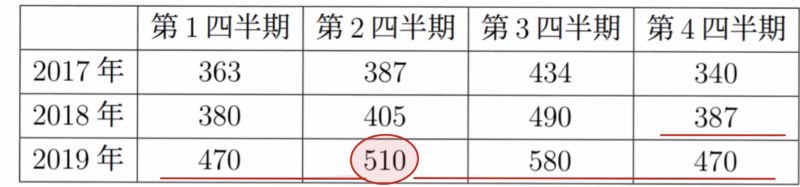
一つ移動平均の計算をしてみよう．次の表はある遊園地における四半期別の入場者を示したものである(単位は千人)．2019年第2四半期における四半期移動平均(中心化4項移動平均)を求めてみよう．

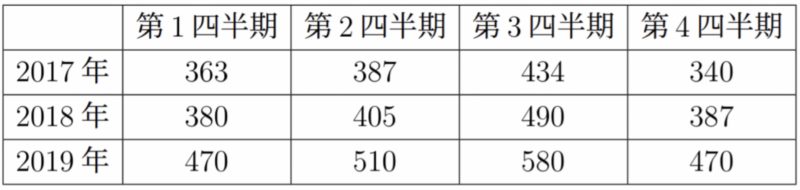
四半期移動平均は，期間が偶数個のため，387,470,510,580,470について，両端の387,470をそれぞれ半分にして足し，４で割ればよい．よって

$$\frac{387/2+470+510+580+470/2}{4}\fallingdotseq 497$$

本ブログ・解説動画に対応した資料です(note)

この記事の動画解説版はこちら↓