変数の種類

この記事の動画解説版はこちら→統計チャンネル

統計学で用いられる変数の種類を尺度というが，尺度は次のように４つに分類される．

表の下にいくほど高次の尺度とされ、扱える計算の種類が増える．それぞれの変数の特徴の違いに着目するとよい．

名義尺度は性別や血液型、電話番号など区別をすることができる尺度(というか区別しかできない尺度)である．血液型の例でいうと「A型の方がO型よりも優れている」というようなことはないから，名義尺度は優劣のような順序の意味をもっていない．

順序尺度では好みの評価やマラソンの着順のように、優劣などによって順序を考えることができる．ただし，「マラソンの1位の選手と3位の選手の差は11位の選手と13位の選手の差に等しい」というようなことはふつう考えない．すなわち順序尺度では差に意味はないとされる．

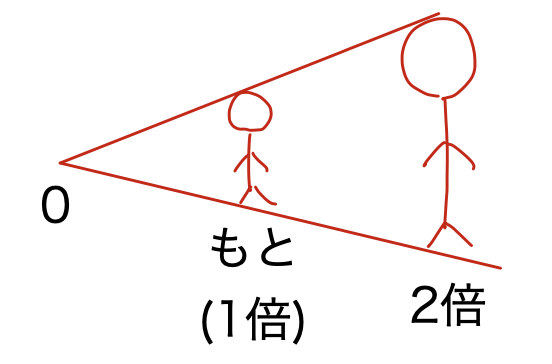
間隔尺度では温度や偏差値のように，間隔(=差)に意味がある．しかし，比には意味はない．この例が最も重要であるが，例えば気温が「10℃」から「20℃」に上がると「10℃上昇した」といいうことはあっても、「2倍に上昇した」という表現はしない．そもそも比の計算，すなわち掛け算や割り算は拡大・縮小に対応している計算のため、掛け算や割り算を考えるためには，0という値が基準として特別な意味を持っている必要がある．例えば数直線上で2という数を3倍する計算を考えると，原点(0の位置)を基準にして右側にビヨーンと伸ばす計算をしていることがわかる．

比を考えることができる尺度を比率尺度(比例尺度，比尺度とも)という．比率尺度は0が基準として特別な意味をもつことだと説明したが，これは「0が何もないことを意味する」とか「原則的にマイナスが存在しない」などと考えると大体うまくいく．間隔尺度である温度や偏差値は負の値をとることはある(偏差値はその定義の仕方から，高得点者が多い状況で低い点数をとると負の値になる場合がある)が，比率尺度である体重や身長が負の値をとることは原則としてない．

以上の４尺度においては，上から下にいくほど利用できる計算が増えていく．順序尺度以降は順番に並べることができるから中央値(〇〇を参照)を考えることができる．間隔尺度以降は差，すなわち足し算や引き算を考えることができるから中央値に加えて平均や標準偏差(〇〇を参照)を考えることができる．比率尺度では比、すなわち掛け算や割り算を考えることができるから相乗平均(〇〇を参照，掛け算ベースの平均のこと)を考えることができる．

ここまで４つの尺度について述べたが，現実に存在するあらゆる量を４つのいずれかの尺度に明確に分類することは困難な場合もある．例えば中学校や高等学校で広く行われている５段階評定において「評定1と評定3の差は評定3と評定5の差と等しい」と言えるかは微妙で，原理主義的に考えれば評定は順序尺度であるから，差や和の計算には意味がないことになる．しかし現実では，評定の差に意味があるものとみなして評定平均などを考えている(大学の成績に関するGPA制度も本質的に同じ話である)．このように，現実に登場する量において，各尺度の境界は実際にはそれほど明瞭ではなく，それほど神経質に分類に拘らなくてもよい(と思う)．

ここまで４つの尺度について述べたが，別の分類方法として名義尺度，順序尺度をまとめて質的変数，間隔尺度，比率尺度をまとめて量的変数という言い方がある．少しごちゃごちゃしてきたので今まで述べたことを全部表にまとめておく．

最後に，量的変数の別の分け方も紹介しておく．ある範囲の値を連続的にとる量を連続変数という．例えば身長は観測ではどうしても読み取る数値の制度に限界があり，小数第1位で丸めることが多いが，生身の人間の身長としては173.14804766…cmなどといくらでも細かい数値をとることができるから，連続変数である．一方とびとびの値しかとらない変数を離散変数という．何かの実験の成功回数，特定の条件を満たす人数などは値として整数$0,1,2,3,\cdots $しかとらないから離散変数である．

本ブログ・解説動画に対応した資料です(note)

この記事の動画解説版はこちら↓