仮説検定の一般的な手順

この記事の動画解説版はこちら→統計チャンネル

仮説のもとで，実現値が統計的に極端な値かどうか判断し，極端な場合は仮説を否定することで統計的な主張を行うのが仮説検定である．例題を通して，仮説検定の手順を紹介する．

(例)機械Aが製造するある部品の重量は平均$\mu=9.5$ (g)の正規分布に従うとされていたが，最近になって製造方法に変更を加えたところ，重量が大きくなったという報告が上がった．そこで，この部品について7個を無作為に選び，重量(g)を計測すると，以下の通りになった．製造方法の変更で平均 $\mu$ の値が $9.5$ より増大したといえるかどうかを有意水準5%で検定せよ．なお，母分散は$\sigma^2=0.7^2$とせよ．

(STEP 0) 最初に有意水準を設定

「有意水準$5\%$で検定せよ」との問題文の指定により，有意水準は$5\%$とする(STEP3の棄却域の設定で基準として用いる)．

(STEP1) 母集団分布と，興味のある母数の確認に加えて，帰無仮説と対立仮説を設定

今回の母集団分布は正規分布$\mbox{N}(\mu, 0.7^2)$，最終的には$\mu$が$9.5$より大きいと言えるか知りたい状況である．そこで，帰無仮説を$\mu=9.5$，対立仮説を$\mu>9.5$と設定する．

(STEP 2)帰無仮説$H_0$のもとで，興味のある母数を含む統計量の分布を調べる

今回は平均重量(母平均$\mu$)に興味があるので，標本平均の分布を確認する．

　$ \displaystyle　\overline{X}=\frac{X_1+X_2+\cdots +X_7}{7}\sim \mbox{N}\left(\mu, \frac{\sigma^2}{7}\right)$

標準化すれば $ \displaystyle Z=\frac{\overline{X}-\mu}{\sqrt{\sigma^2/7}}\sim \mbox{N}(0,1)$

よって帰無仮説の仮定のもとでは
$ \hspace{5mm}\rule[-1mm]{0mm}{7.5mm} \displaystyle Z=\frac{\overline{X}-9.5}{\sqrt{\sigma^2/n}}\sim \mbox{N}(0,1)$

(STEP 3)棄却域の設定と実現値のを計算し，結論する

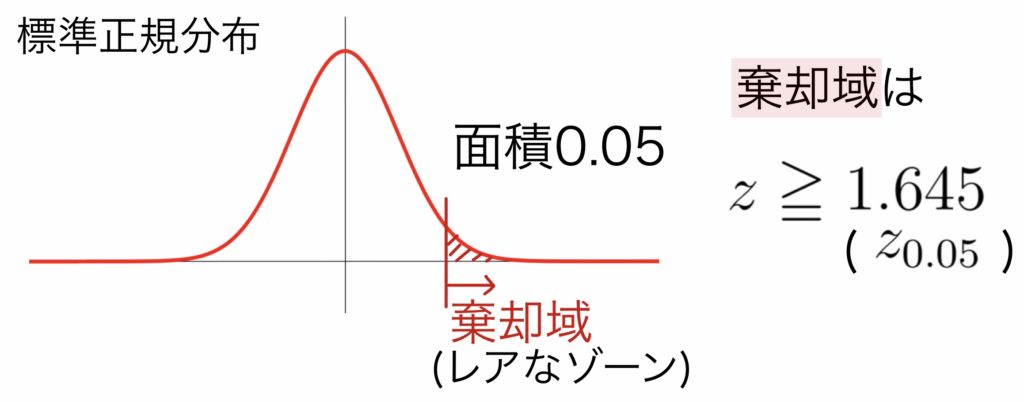
棄却域は$z\geqq 1.645 (=z_{0.05})$となる．

$\hspace{5mm}\rule[-1mm]{0mm}{7.5mm} \displaystyle z=\frac{9.8-9.5}{\sqrt{0.7^2/7}}=1.13\cdots (<1.645)$

この値は棄却域に含まれない($1.645$未満)ので，有意水準$5\%$で$H_0$は棄却されない．すなわち製造方法の変更で平均が$9.5$(g)より増大したとは言えない．

本ブログ・解説動画に対応した資料です(note)

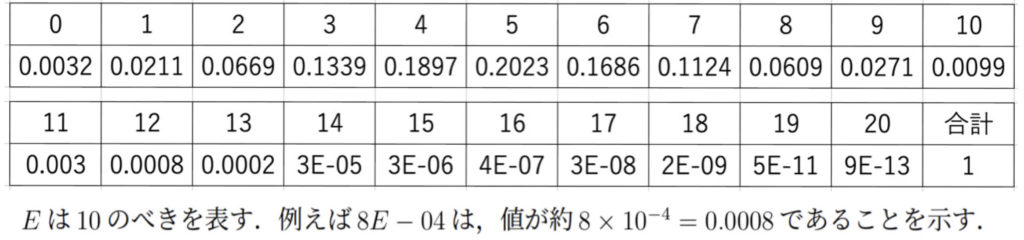
この記事の動画解説版はこちら↓