よく使う区間推定一覧(2標本)

この記事の動画解説版はこちら→統計チャンネル
区間推定の手法(2標本)の一覧をまとめる.信頼区間の形は母集団分布と興味のある母数の組み合わせから計算できる.なお、2標本の場合,実用上は区間推定よりも検定(記事44,45)を行うことの方が多い.
母集団分布と,興味のある母数

※ ここでは大前提として2変数$X,Y$に対応がない場合を考えている.対応がある場合はその差を改めて1つの変数とみなして1標本の母平均の推定に帰着させる.
対応する統計量と信頼区間はこちら
${\sigma_{A}}^2, {\sigma_{B}}^2$が既知のとき
\( Z=\frac{(\overline{X}-\overline{Y})-(\mu_A-\mu_B)}{\sqrt{\frac{{\sigma_A}^2}{n_A}+\frac{{\sigma_B}^2}{n_B}}}\sim \mbox{N}(0,1) \)
信頼区間は
\( (\mbox{☆}) \cdots (\overline{x}-\overline{y})\!-\!z_{\alpha/2}\!\cdot\! \sqrt{\frac{{\sigma_{A}}^{\!2}}{n_A}+\frac{{\sigma_{B}}^{\!2}}{n_B}} \leqq \mu_A-\mu_B \leqq (\overline{x}-\overline{y})\!+\!z_{\alpha/2}\!\cdot\! \sqrt{\frac{{\sigma_{A}}^{\!2}}{n_A}+\frac{{\sigma_{B}}^{\!2}}{n_B}}\)

${\sigma_{A}}^2={\sigma_{B}}^2$のとき
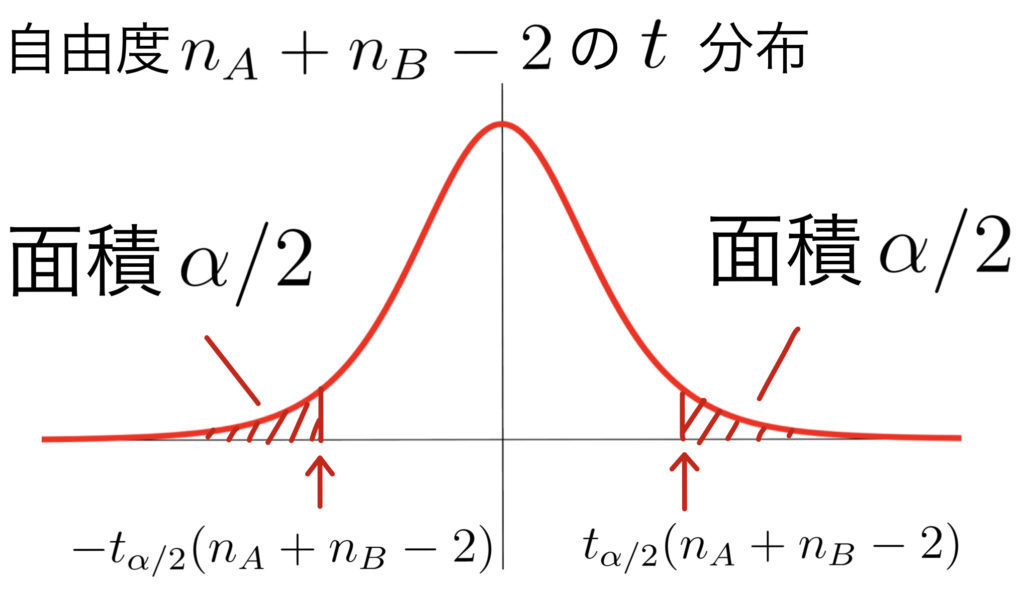
\( T=\frac{(\overline{X}-\overline{Y})-(\mu_A-\mu_B)}{\sqrt{\frac{U^2}{n_A}+\frac{U^2}{n_B}}}\sim t(n_A+n_B-2) \)
ただし$U^2$は次式(プールされた分散,合併分散などという)
\( \displaystyle U^2=\frac{(n_A-1){U_{\!A}}^2+(n_B-1){U_{\!B}}^2}{n_A+n_B-2}\)
信頼区間は($\mbox{☆}$)で${\sigma_{A}}^2, {\sigma_{B}}^2$をともに$u^2$,$z_{\alpha/2}$を$t_{\alpha/2}(n_A\!+\!n_B\!-\!2)$に取り替えたもの.
分散の情報なしのとき
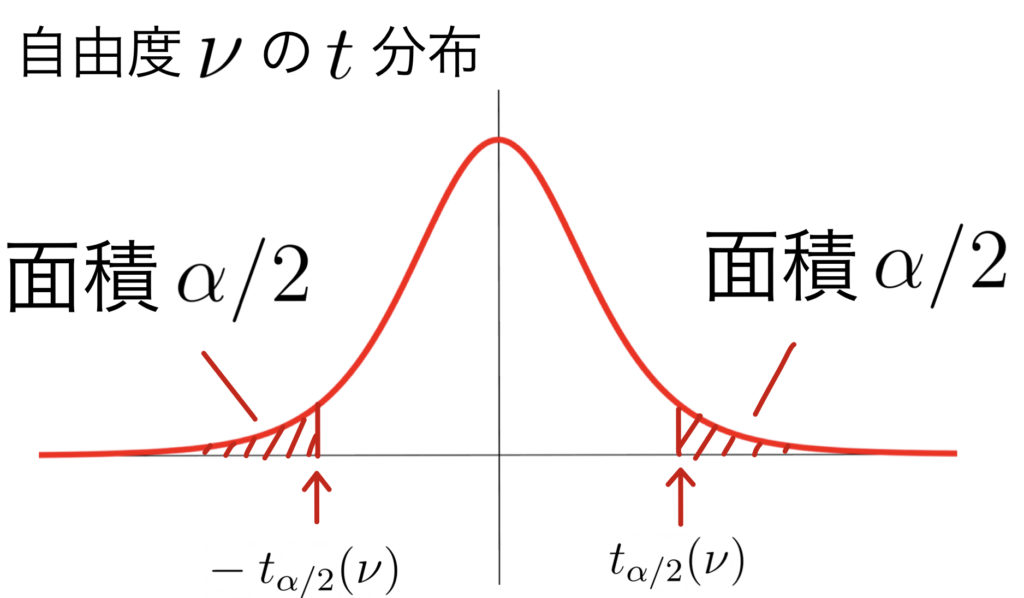
\( \displaystyle T=\frac{(\overline{X}-\overline{Y})-(\mu_A-\mu_B)}{{\sqrt{\frac{{U_A}^2}{n_A}+\frac{{U_B}^2}{n_B}}}}\sim t(\nu) \)
ただし,$\nu$は以下の値に一番近い整数
\( \displaystyle \rule[-1mm]{0mm}{7.5mm}\nu=\frac{\left(\frac{{u_A}^2}{n_A}+\frac{{u_B}^2}{n_B}\right)^2}{\frac{({u_A}^2/n_A)^2}{n_A-1}+\frac{({u_B}^2/n_B)^2}{n_B-1}}\)
信頼区間は($\mbox{☆}$)で${\sigma_{A}}^2, {\sigma_{B}}^2$をそれぞれ${u_A}^2,{u_B}^2$,$z_{\alpha/2}$を$t_{\alpha/2}(\nu)$に取り替えたもの.

対応する統計量と信頼区間はこちら
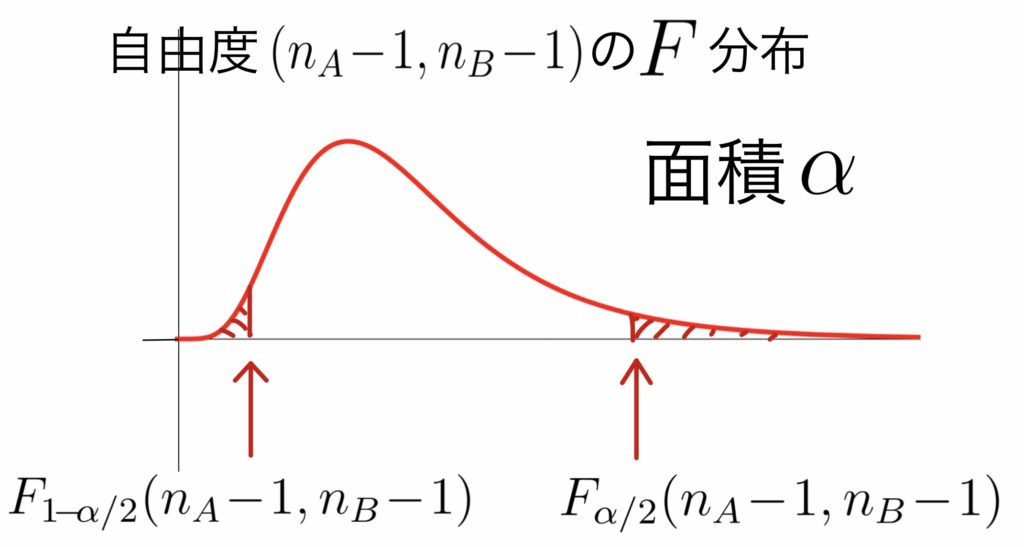
\( \displaystyle \rule[-1mm]{0mm}{7.5mm} \chi^2=\frac{(n-1)U^2}{\sigma^2}\sim \chi^2(n-1) \)
$\rule[-1mm]{0mm}{7.5mm}$信頼区間は
\( \displaystyle \rule[-1mm]{0mm}{7.5mm} \frac{(n-1)\!\cdot\!u^2}{{\chi^2}_{\!\!\alpha/2}(n-1)}\leqq\sigma^2\leqq \frac{(n-1)\!\cdot\!u^2}{{\chi^2}_{\!\!1-\alpha/2}(n-1)}\)

対応する統計量と信頼区間はこちら
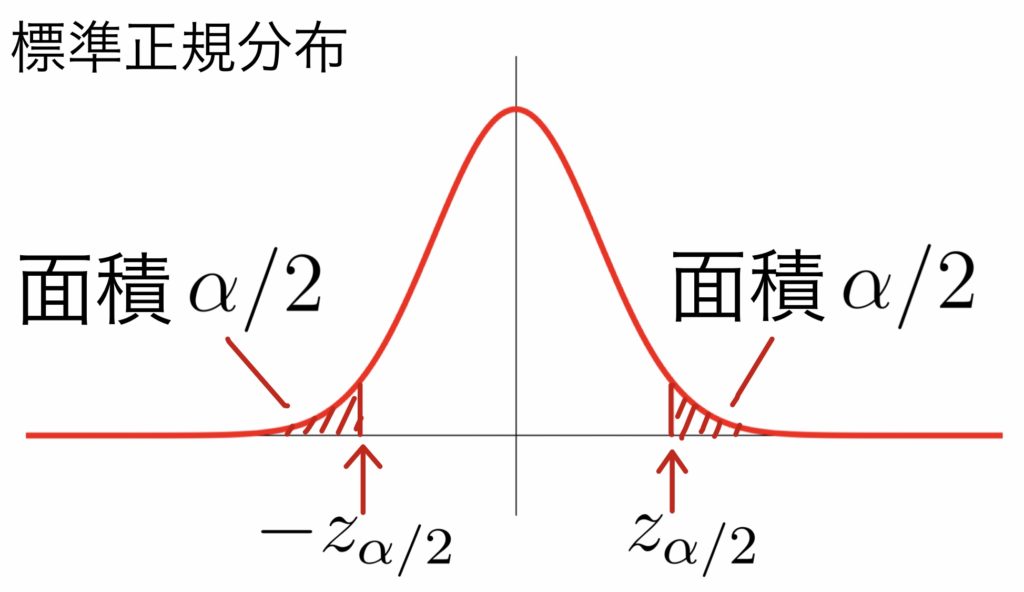
\( \displaystyle \rule[-1mm]{0mm}{7.5mm}Z\!=\!\frac{(\hat{P_A}-\hat{P_B})-(p_A-p_B)}{\sqrt{\frac{p_A(1-p_A)}{n_A}+\frac{p_B(1-p_B)}{n_B}}}\sim \mbox{N}(0,1) \)
信頼区間は
\( \displaystyle \rule[-1mm]{0mm}{7.5mm}(\hat{p}_A\!-\!\hat{p}_B)\!-\!z_{\alpha/2}\!\cdot\!\sqrt{\cdots}\leqq p_A\!-\!p_B\leqq(\hat{p}_A\!-\!\hat{p}_B)\!+\!z_{\alpha/2}\!\cdot\!\sqrt{\cdots}\)
$\rule[-1mm]{0mm}{11.5mm}$※ $\cdots $には$ \displaystyle \frac{\hat{p}_A(1\!-\!\hat{p}_A)}{n_A}\!+\!\frac{\hat{p}_B(1\!-\!\hat{p}_B)}{n_B}$が入る.
※根号内の $p_A,p_B$ は推定値 $\hat{p}_A, \hat{p}_B$ に置き換えている.
問1
ある成分の原料産地としてA,Bの2つの産地から見本原料の純度を測定した結果が以下表である.A,Bでの見本原料の純度はそれぞれ平均 $\mu_A, \mu_B$ の正規分布に従い,分散は等しいと仮定した上で $\mu_A-\mu_B$ の$95\%$ 信頼区間として最も適当なものを選択肢から選べ.

【選択肢】
$\ \mbox{①} -0.39\leqq\mu_A-\mu_B\leqq 1.81$
$\ \mbox{②} -0.19\leqq\mu_A-\mu_B\leqq 2.01$
$\ \mbox{③}\ -0.11\leqq\mu_A-\mu_B\leqq 2.31$
解答はこちら
解
産地A,Bの見本原料の純度をそれぞれ$X_i$,$Y_i$とおくと,仮定により
$\hspace{2mm}\rule[-1mm]{0mm}{7.5mm} \displaystyle X_{ i}\sim\mbox{N}(\mu_A, {\sigma_{A}}^2)$
$\hspace{2mm}\rule[-1mm]{0mm}{7.5mm} \displaystyle Y_{ i}\sim \mbox{N}(\mu_B,{\sigma_{B}}^2)$
$\hspace{2mm}\rule[-1mm]{0mm}{7.5mm} \displaystyle \overline{X}= \sum_{i=1}^{26}X_{ i}\sim\mbox{N}\left(\mu_A, \frac{{\sigma_{A}}^2}{26}\right)$
$\hspace{2mm}\rule[-1mm]{0mm}{7.5mm} \displaystyle \overline{Y}= \sum_{i=1}^{16}Y_{i}\sim\mbox{N}\left(\mu_B, \frac{{\sigma_{B}}^2}{16}\right)$
であるから
$\hspace{2mm}\rule[-1mm]{0mm}{7.5mm} \displaystyle \overline{X}-\overline{Y}\sim\mbox{N}\left(\mu_A-\mu_B, \frac{{\sigma_{A}}^2}{26}+\frac{{\sigma_{B}}^2}{16}\right)$
標準化すれば
$\hspace{2mm}\rule[-1mm]{0mm}{7.5mm} \displaystyle \frac{\overline{X}-\overline{Y}-(\mu_A-\mu_B)}{\sqrt{\frac{{\sigma_{A}}^2}{26}+\frac{{\sigma_{B}^2}}{16}}}\sim \mbox{N}(0,1)$
となる.いま,${\sigma_{A}}^2={\sigma_{B}}^2$としてよいから,${\sigma_{A}}^2,{\sigma_{B}}^2$を次のプールした分散
$\hspace{2mm}\rule[-1mm]{0mm}{7.5mm} \displaystyle U^2=\frac{(n_A-1){U_{A}}^2+(n_B-1){U_{B}}^2}{n_A+n_B-2}$
$\hspace{11mm}\rule[-1mm]{0mm}{7.5mm} \displaystyle =\frac{25{U_{\!A}}^2+15{U_{\!B}}^2}{40}$
に取り替えると
$\hspace{2mm}\rule[-1mm]{0mm}{10.5mm} \displaystyle \frac{\overline{X}-\overline{Y}-(\mu_A-\mu_B)}{\sqrt{\frac{U^2}{26}+\frac{{U^2}}{16}}}\sim t(n_A+n_B-2)=t(40)$
となる.$95\%$信頼区間は
$\hspace{2mm}\rule[-1mm]{0mm}{7.5mm} \displaystyle -2.021\leqq \frac{\overline{X}-\overline{Y}-(\mu_A-\mu_B)}{\sqrt{\frac{U^2}{26}+\frac{{U^2}}{16}}}\leqq 2.021$
すなわち
$\hspace{2mm}\rule[-1mm]{0mm}{10.5mm} \displaystyle \overline{X}-\overline{Y}-2.021\sqrt{\frac{U^2}{26}+\frac{{U^2}}{16}}\leqq \mu_A-\mu_B\leqq \overline{X}-\overline{Y}+2.021\sqrt{\frac{U^2}{26}+\frac{U^2}{16}}$
となる.実現値 $\overline{x}-\overline{y}=8.6-7.5=1.1$ ,$\displaystyle u^2=\frac{25\cdot 3.48+15\cdot 3.68}{40}=3.555$ により $-0.110\cdots \leqq \mu_A-\mu_B\leqq 2.310\cdots $ となるから,$\mbox{③}$が適する.
問2
あるビニールハウスで,品種Aの種子 $100$ 個と,品種Bの種子$120$ 個をまき,同一条件下で発芽するかどうかの実験を行った.一定期間後に発芽したのは品種Aでは $90$ 個,品種Bでは $80$ 個が発芽した.品種A,Bの発芽率を$p_A,p_B$とするとき,その発芽率の差$p_A-p_B$に対する $95\%$ 信頼区間として最も適当なものを選択肢から選べ.
【選択肢】
$\ \mbox{①} \ -0.06\leqq p_A-p_B\leqq 0.16$
$\ \mbox{②} \ 0.13 \leqq p_A-p_B\leqq 0.34$
$\ \mbox{③} \ 0.25\leqq p_A-p_B\leqq 0.55$
解答はこちら
解
品種A,Bが発芽するかどうかに対応する確率変数をそれぞれ
$\hspace{2mm}\rule[-1mm]{0mm}{7.5mm} \displaystyle X_{ i}\sim \mbox{Be}(p_A)$,
$\hspace{2mm}\rule[-1mm]{0mm}{7.5mm} \displaystyle Y_{ i}\sim \mbox{Be}(p_B)$
とおく.中心極限定理により近似的に
$\hspace{2mm}\rule[-1mm]{0mm}{7.5mm} \displaystyle \hat{P_A}=\frac{1}{100}\sum_{i=1}^{100}X_{ i}\sim\mbox{N}\left(p_A, \frac{p_A(1-p_A)}{100}\right)$
$\hspace{2mm}\rule[-1mm]{0mm}{7.5mm} \displaystyle \hat{P_B}=\frac{1}{120}\sum_{i=1}^{120}Y_{i}\sim \mbox{N}\left(p_B, \frac{p_B(1-p_B)}{120}\right)$
であるから,
$\hspace{2mm}\rule[-1mm]{0mm}{7.5mm} \displaystyle \frac{(\hat{P_A}-\hat{P_B})-(p_A-p_B)}{\sqrt{\frac{p_A(1-p_A)}{100}+\frac{p_B(1-p_B)}{120}}}\sim\mbox{N}(0,1)$
となる.$95\%$信頼区間は
$\hspace{2mm}\rule[-1mm]{0mm}{7.5mm} \displaystyle -1.96\leqq \frac{(\hat{P_A}-\hat{P_B})-(p_A-p_B)}{\sqrt{\frac{p_A(1-p_A)}{100}+\frac{p_B(1-p_B)}{120}}} \leqq 1.96$
を$p_A-p_B$について解いて
$\hspace{2mm}\rule[-1mm]{0mm}{10.5mm} \displaystyle (\hat{P_A}-\hat{P_B})-1.96\sqrt{\frac{p_A(1-p_A)}{100}+\frac{p_B(1-p_B)}{120}}\leqq p_A-p_B\leqq (\hat{P_A}-\hat{P_B})+1.96\sqrt{\frac{p_A(1-p_A)}{100}+\frac{p_B(1-p_B)}{120}}$
$\hat{P_A}-\hat{P_B}$は実現値$\rule[-1mm]{0mm}{7.5mm} \displaystyle \hat{p}_A-\hat{p}_B=\frac{90}{100}-\frac{80}{120}=0.233\cdots $,区間の端の母数$p_A, p_B$は$\rule[-1mm]{0mm}{7.5mm} \displaystyle \hat{p}_A=\frac{90}{100}, \hat{p}_B=\frac{80}{120}$に取り替えて信頼区間を計算すると$0.125\cdots \leqq p_A-p_B\leqq 0.341\cdots $,すなわち$\mbox{②}$が適する.

本ブログ・解説動画に対応した資料です(note)
この記事の動画解説版はこちら↓










