この記事の動画解説版はこちら→統計チャンネル
成功確率$p$のベルヌーイ試行を，初めて成功するまで繰り返したときの試行回数$X$の確率分布を幾何分布(Geometric distribution)といい，$\mbox{Ge}(p)$と表す．
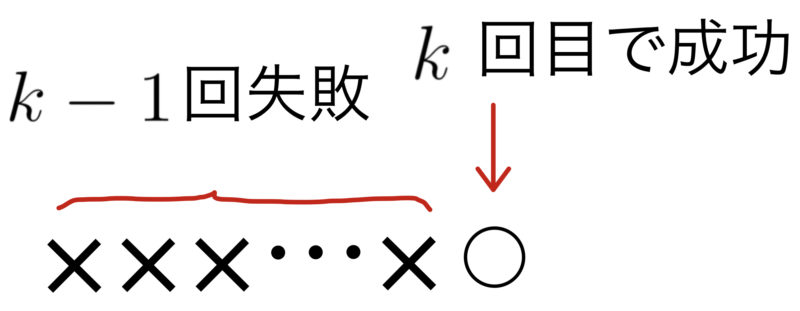
幾何分布の式表示は以下の通り．
\( \displaystyle P(X=k)=pq^{k-1} \)
等比級数の計算などから，幾何分布の期待値と分散は次のようになることが知られている．
$ \displaystyle E(X)=\frac{1}{p},\ V(X)=\frac{q}{p^2}$
(例) ある選手のバスケットボールのフリースローの成功率は$0.8$であり，各試行において成功するか失敗するかは独立とする．初めてフリースローが成功するまでに試行する回数を$X$とおく．このとき，
(1) $P(X=3)$を求めよ． (2) $E(X), V(X)$を求めよ．
解 問題の設定から，$X$は成功確率$p$の幾何分布に従う．
(1) $\displaystyle P(X=3)=0.2^2\times 0.8=0.032$
(2) $\displaystyle E(X)=\frac{1}{0.8}=1.25$
$\displaystyle V(X)=\frac{q}{p^2}=\frac{0.2}{0.8^2}=0.3125 $
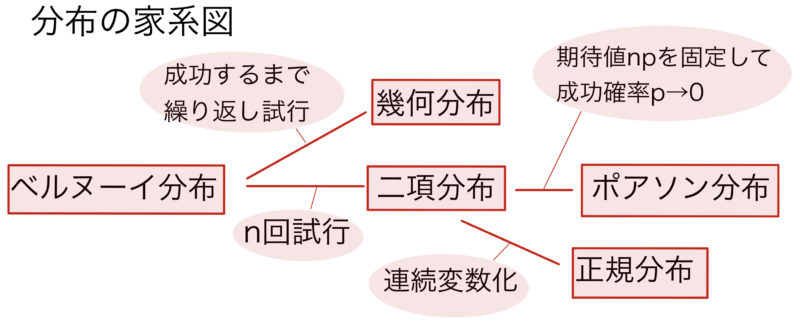
(参考)記事21-25で扱った分布等以下のようにまとめることができる(正規分布は記事27で扱う)．
本ブログ・解説動画に対応した資料です(note)
この記事の動画解説版はこちら↓
| 前の記事へ戻る 24 ポアソン分布 |
次の記事へ 26 連続型確率変数 |
| 記事一覧へ戻る 統計学の基礎シリーズ 目次 |
|