この記事の動画解説版はこちら→統計チャンネル
分布の中心位置は平均,ばらつきの大きさは分散や標準偏差で推し量ることができるが,これらに加えて,分布の非対称性や外れ値の存在を示す指標として,歪度(わいど)や尖度(せんど)を考えることができる.
歪度(わいど)
(確率変数ver.)平均$\mu$,分散$\sigma^2$の確率変数$X$に対して,歪度を\( \displaystyle \frac{E((X-\mu)^3)}{\sigma^3} \) で定義する.正規分布など,左右対象な分布の歪度は0である(ただし,歪度が定義できる分布に限る).
(データver.) $n$個の観測値$x_1,x_2,\cdots, x_n$に対して,歪度を\( \displaystyle \frac{\frac{1}{n}\sum_{i=1}^{n}(x_i-\overline{x})^3}{s^3} \)で定義する.ただし,$s$は標本標準偏差\(\displaystyle\sqrt{\frac{1}{n}\sum_{i=1}^{n}(x_i-\overline{x})^2} \)を意味する.
歪度は偏差の三乗の合計から作られる量である.また,
平均よりも極端に大きい値が存在するとき,偏差の三乗はより大きな正の値になり,
平均よりも極端に小さい値が存在するとき,偏差の三乗はより絶対値の大きい負の値になる.
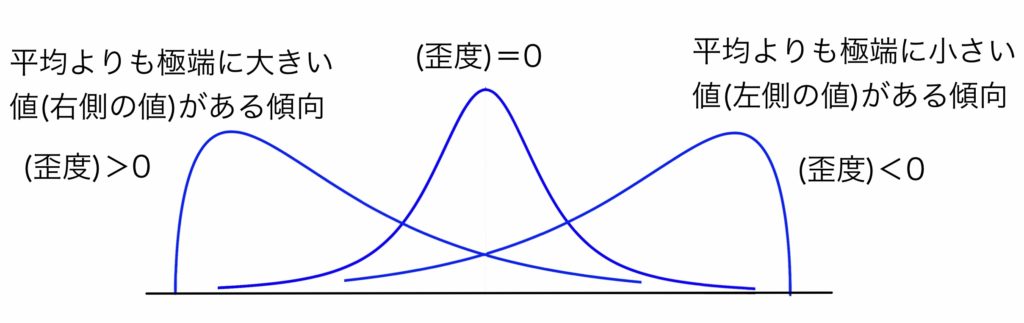
このことから,歪度が正の場合は分布が右に伸びている(右に裾を引くと表現する)傾向,反対に歪度が負の場合は分布が左側に伸びている(左に裾を引くと表現する)傾向があると期待できる.
尖度(せんど)
(確率変数ver.)平均$\mu$,分散$\sigma^2$の確率変数$X$に対して,尖度を\( \displaystyle \frac{E((X-\mu)^4)}{\sigma^4}-3 \) で定義する.正規分布の尖度は0である.
(データver.) $n$個の観測値$x_1,x_2,\cdots, x_n$に対して,尖度を\( \displaystyle \frac{\frac{1}{n}\sum_{i=1}^{n}(x_i-\overline{x})^4}{s^4} \)で定義する.
歪度は偏差の四乗の合計から作られる量である.また,
「平均よりも極端に大きい値または小さい値」,すなわち外れ値が存在するとき,偏差の四乗はより大きな正の値になる
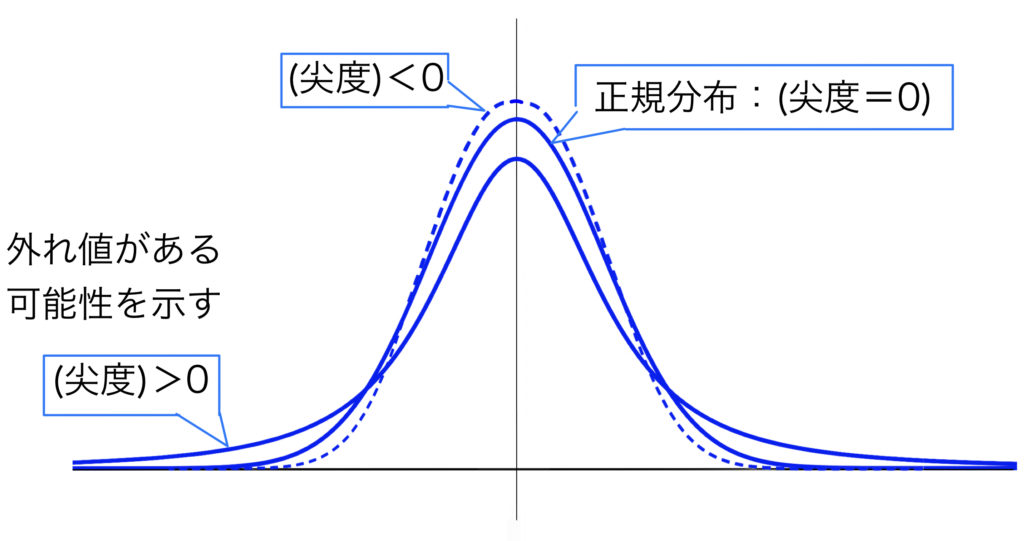
このことから,尖度が正の場合は外れ値が多く,尖度が負の場合は外れ値が少なく平均の周りに値が集中している傾向が期待できる.
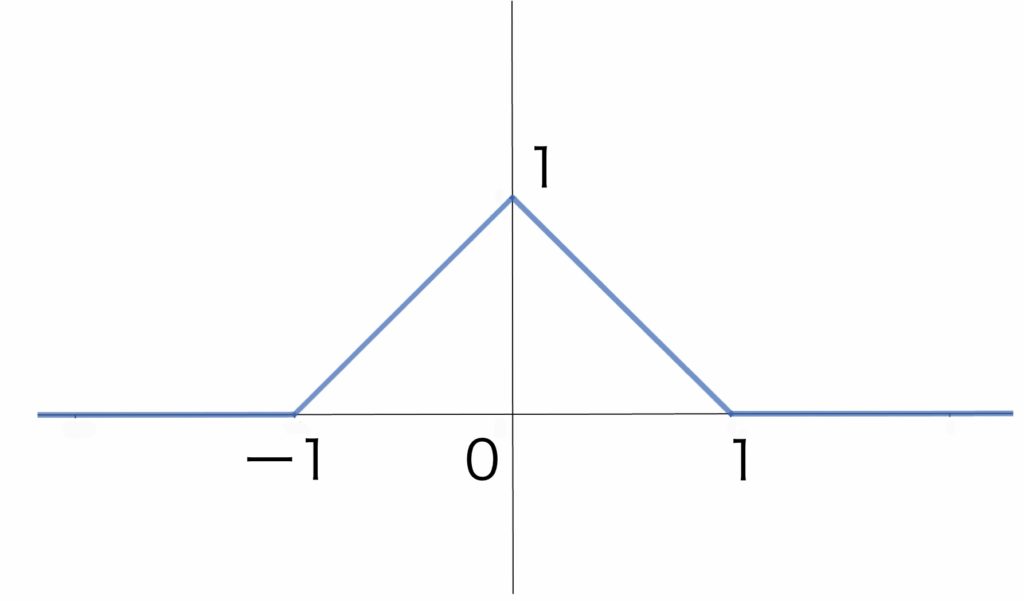
次の密度関数$f(x)$をもつ確率変数$X$について,歪度と尖度を求めよ.
$ \displaystyle f(x)=\begin{cases}
x+1 &(-1\leqq x\leqq 0)\\
-x+1 &(0\leqq x\leqq 1)\\
0 &(\mbox{その他})
\end{cases}$
この記事の動画解説版はこちら↓
| 前の記事へ戻る 31 二項分布の正規分布近似 |
次の記事へ 33 標本 |
| 記事一覧へ戻る 統計学の基礎シリーズ 目次 |
|