抽出方法

この記事の動画解説版はこちら→統計チャンネル

標本の抽出の仕方として，代表的なものを5つ述べる．実際の調査では，複数の手法を組み合わせることが多い．

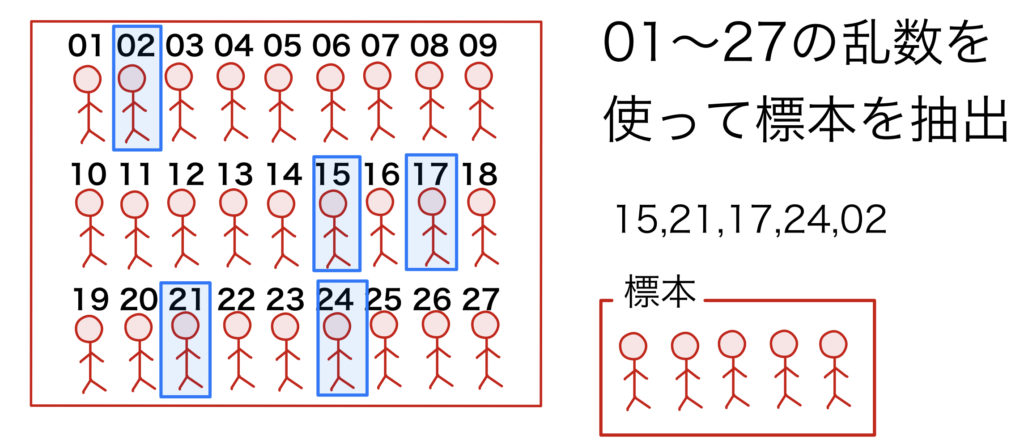
(1)単純無作為抽出法

偏りが少ない理想的な標本を作成することができる．手順としては以下の通り．
(i)母集団の構成要素に一連の通し番号をつける
(ii)乱数表などから標本サイズ(標本に含まれる要素の数)と同じ数の乱数を取り出し，対応する要素を抽出する
この方法は母集団のサイズが大きい場合には実用的とは言えないことがある．例えば，日本在住者を母集団とした調査を実施する場合，通し番号をつけるのも困難(日本なら1億以上！)な上，乱数も大量に必要とし，さらに調査対象として標本に含まれる世帯がいろいろな地域にバラバラに抽出されてしまい，調査に大きな費用や時間がかかってしまう．

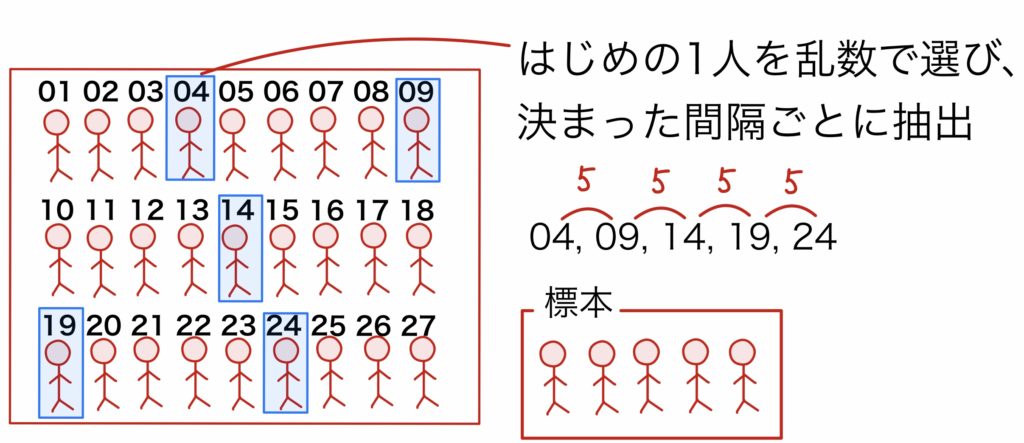
(2)系統抽出法

系統抽出法は，乱数を大量に用意する手間を省く方法と言える．最初の乱数を決めるまでは(1)と同じだが，要素の2つめ以降は決まった間隔ごとに抽出する(特に等間隔抽出法とも)．間隔としては，通し番号全体からまんべんなく抽出するために，母集団のサイズ÷標本のサイズぐらいにするとよいだろう(例えば母集団の要素が5000，標本のサイズが100なら50刻みにするなど)．前提として，通し番号をつけるときに周期性がないことが必要である．例えば通し番号を男女交互につけて偶数間隔ごとの抽出を行うと，同じ性別のみが集まった(偏った)標本となってしまう．

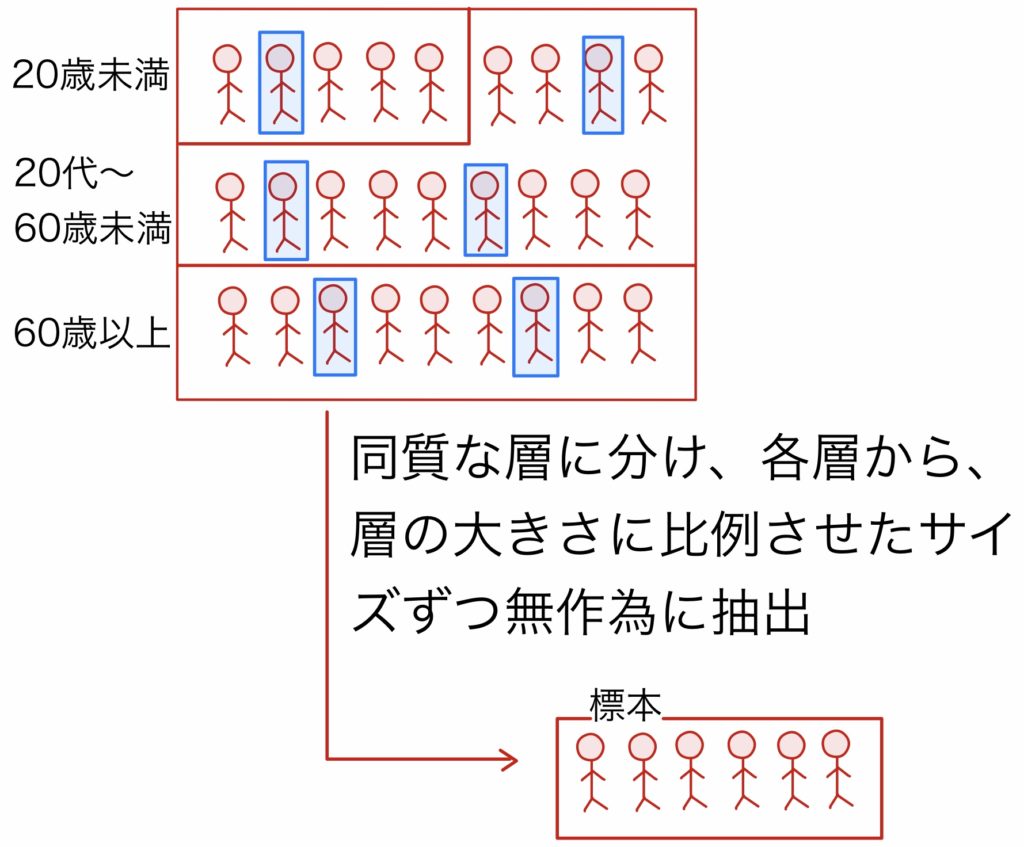
(3)層化無作為抽出法

母集団が性別・年代別・職業別などいくつかの異なる種類にグループ(層)化される場合，それぞれのグループごとに無作為に抽出する方法．グループのサイズなどによって，各グループから抽出する要素数を定める．層化されたグループのリストが最初から用意されているような場合や簡単に作成できるような場合に有用である．

(4)多段抽出法

調査の手間や費用を小さくするためには，できる限りまとまった地域で調査ができると都合がよいが，標本の精度のために，地域特性による標本の偏りも排除したい．そこで次のような多段抽出とよばれる方法がよく用いられる．大きな抽出単位からはじめて，目的である小さな抽出単位へ段階を追って単純無作為抽出を重ねる．一般に，段数を重ねるごとに精度の低下につながりやすい(以下の例は2段抽出)．

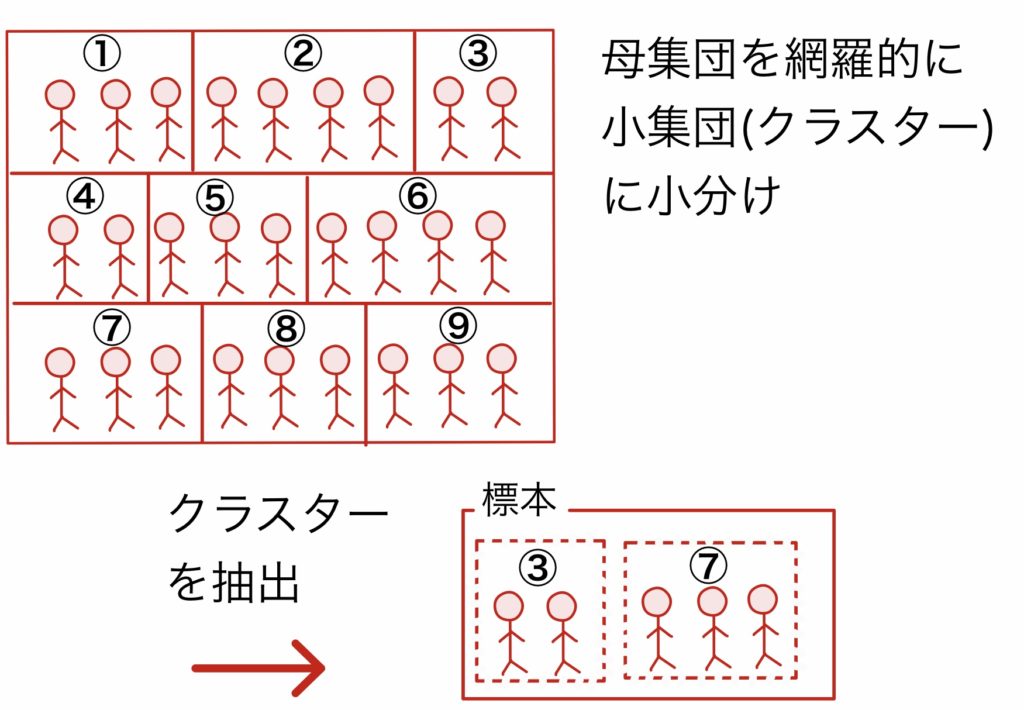
(5)クラスター抽出法(集落抽出法)

母集団を網羅的に小集団(クラスター)に小分けし，クラスターを抽出し，そのクラスターの集まりを丸ごと標本とする．例えば高校生に対しての調査で全国の各高校をクラスターと考え，いくつかの高校を抽出，選ばれた高校の生徒全員がその調査に協力するなど．クラスターとしてまとまりがあるため調査が実施しやすいのはメリットであるが，クラスター内が同じ特性をもつ場合，標本の偏りが大きくなる．先ほどの例の場合，クラスターとして男子校・女子校を抽出した場合は性別による偏りが強くなると考えられる．

本ブログ・解説動画に対応した資料です(note)

この記事の動画解説版はこちら↓