よく使う仮説検定一覧(2標本)その1

この記事の動画解説版はこちら→統計チャンネル
よく使う仮説検定の手法(2標本)の一覧をまとめる.(検定)統計量の形は母集団分布と興味のある母数の組み合わせから計算できる.
母集団分布,興味のある母数,仮説

$H_0: \mu_A=\mu_B, H_1: \mu_A>\mu_B$
※ ここでは大前提として2変数$X,Y$に対応がない場合を考えている.対応がある場合はその差を改めて1つの変数とみなして1標本の母平均の推定に帰着させる(記事44の問題2を参照).
対応する検定統計量,棄却域はこちら
${\sigma_{A}}^2, {\sigma_{B}}^2$が既知のとき
$\rule[-1mm]{0mm}{7.5mm} \displaystyle Z=\frac{\overline{X}-\overline{Y}}{\sqrt{\frac{{\sigma_A}^2}{n_A}+\frac{{\sigma_B}^2}{n_B}}}\sim \mbox{N}(0,1)$
$\rule[-1mm]{0mm}{10.5mm}$棄却域は \( \displaystyle \rule[-1mm]{0mm}{7.5mm} z\geqq z_{\alpha}\)
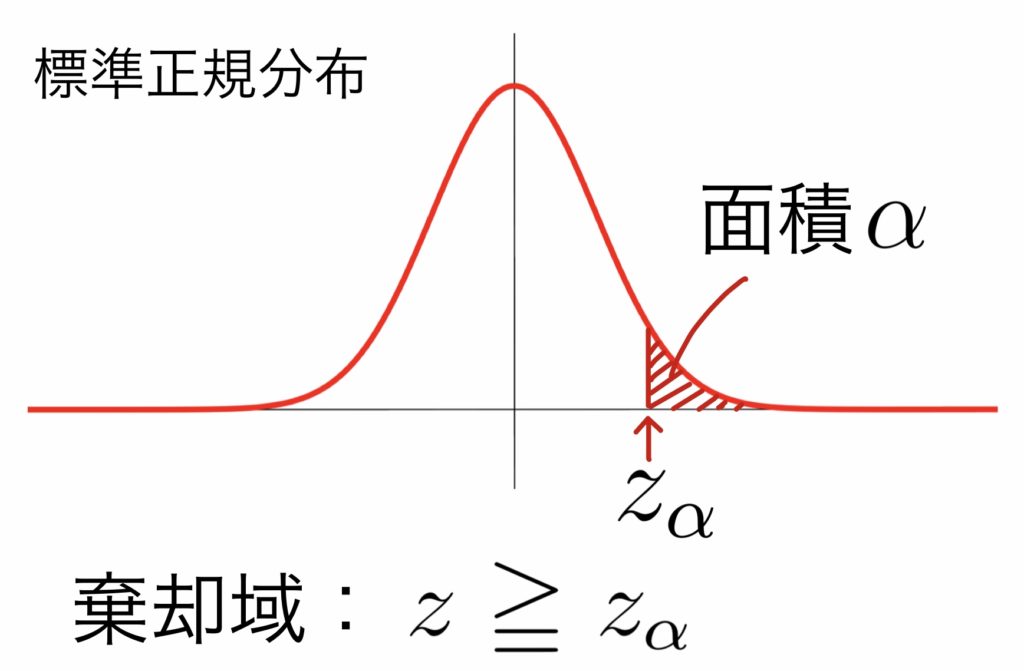
${\sigma_{A}}^2={\sigma_{B}}^2$のとき
\( \displaystyle T=\frac{\overline{X}-\overline{Y}}{\sqrt{\frac{U^2}{n_A}+\frac{U^2}{n_B}}}\sim t(n_A+n_B-2) \)
ただし
\( \displaystyle U^2=\frac{(n_A-1){U_{\!A}}^2+(n_B-1){U_{\!B}}^2}{n_A+n_B-2}\)
棄却域は$t\geqq t_{\alpha}(n_A+n_B-2)$
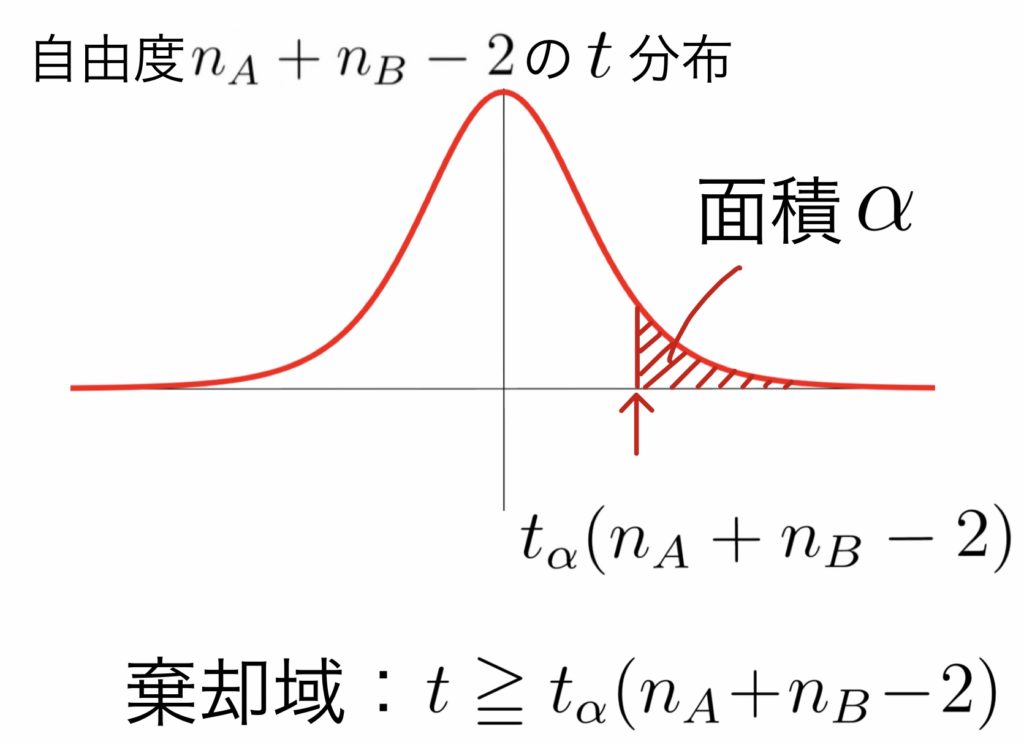
分散の情報なしのとき (ウェルチの検定という)
\( \displaystyle T=\frac{\overline{X}-\overline{Y}}{{\sqrt{\frac{{U_A}^2}{n_A}+\frac{{U_B}^2}{n_B}}}}\sim t(\nu) \)
ただし,$\nu$は以下の値に一番近い整数
\( \displaystyle \rule[-1mm]{0mm}{7.5mm}\nu=\frac{\left(\frac{{u_A}^2}{n_A}+\frac{{u_B}^2}{n_B}\right)^2}{\frac{({u_A}^2/n_A)^2}{n_A-1}+\frac{({u_B}^2/n_B)^2}{n_B-1}}\)
棄却域は$t\geqq t_{\alpha}(\nu)$
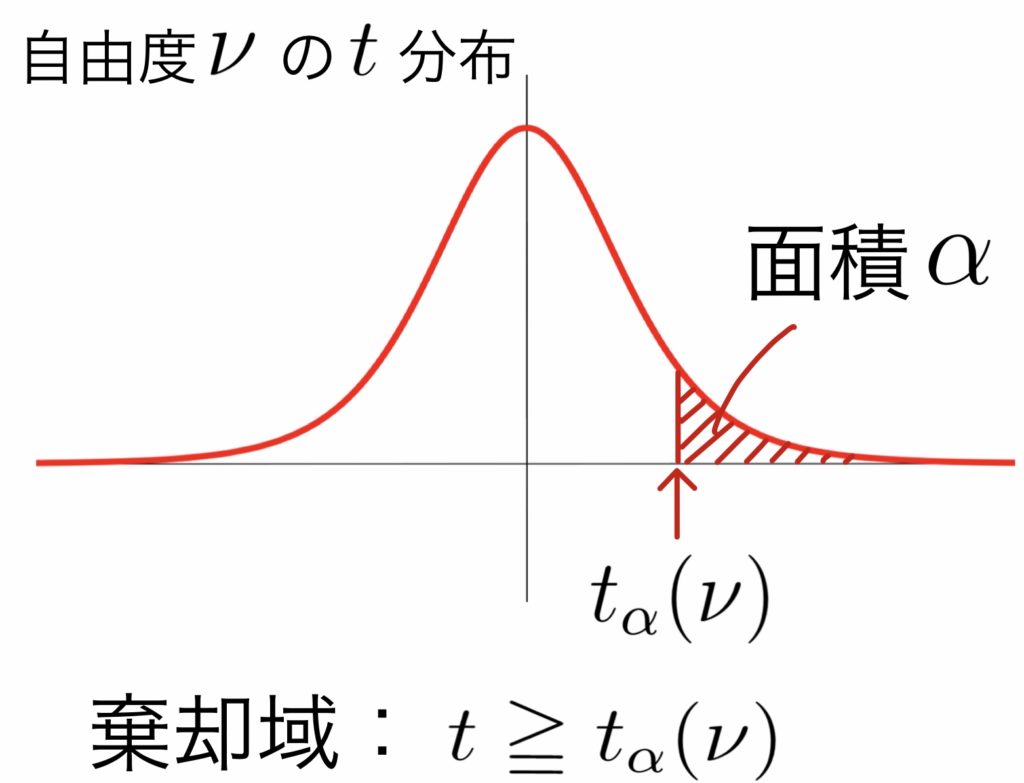

$H_0: \sigma_A=\sigma_B, H_1: {\sigma_A}^2>{\sigma_B}^2$
対応する検定統計量,棄却域はこちら
\( \displaystyle \rule[-1mm]{0mm}{7.5mm} F=\frac{{U_A}^2}{{U_B}^2}\sim F(n_A-1, n_B-1) \)
$\rule[-1mm]{0mm}{7.5mm}$ 棄却域は \( \displaystyle \rule[-1mm]{0mm}{7.5mm} f\geqq F_{\alpha}(n_A\!-\!1,n_B\!-\!1)\)
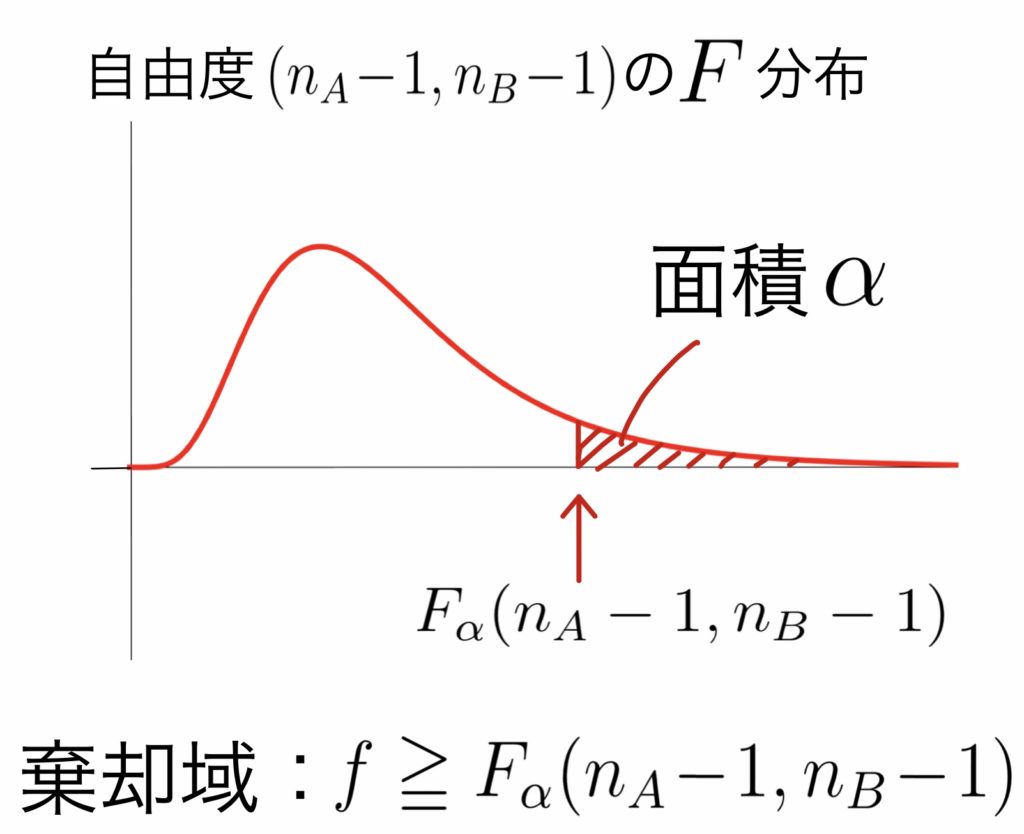
※両側検定のときは統計量${U_A}^2, {U_B}^2$のうち大きい方を分子にして,棄却域を右側にとる(面積は$\alpha/2$とする)

対応する検定統計量,棄却域はこちら
\( \displaystyle \rule[-1mm]{0mm}{7.5mm}Z\!=\!\frac{\hat{P_A}-\hat{P_B}}{
\sqrt{\frac{p_A(1- p_A)}{n_A}+\frac{p_B(1- p_B)}{n_B}}
}\sim \mbox{N}(0,1) \)
$\rule[-1mm]{0mm}{10.5mm}$棄却域は \( \displaystyle \rule[-1mm]{0mm}{7.5mm} z\geqq z_{\alpha}\)
※根号内の $p_A,p_B$ は推定値 $\hat{p}_A, \hat{p}_B$ に置き換えるなどして計算する(別の方法については
次記事の問2を参照).

問1
A大学の大学院のある専攻では,大学院入試にてA大学出身の学生が5名,他大学出身の学生が $6$ 名大学院入試を受験し,$100$ 点満点の学力試験で以下のような結果になった.A大学出身の学生の方が成績が良いと考えてよいか有意水準5%で検定せよ.ただし,成績はいずれの場合も正規分布に従うものとし,各分布の分散は等しいと仮定してよいものとする.

解答はこちら
解
A大学出身者,他大学出身者の成績の分布をそれぞれ
$\hspace{2mm}\rule[-1mm]{0mm}{7.5mm} \displaystyle \mbox{N}(\mu_A, {\sigma_A}^2), \mbox{N}(\mu_B, {\sigma_B}^2)$
とする.A大学出身者の成績が良いか検証したいのだから,
$\hspace{2mm}\rule[-1mm]{0mm}{7.5mm} \displaystyle H_0: \mu_A=\mu_B$,$H_1: \mu_A>\,u_B$
とすればよい.
$\hspace{2mm}\rule[-1mm]{0mm}{7.5mm} \displaystyle X_{i}\sim\mbox{N}(\mu_A, {\sigma_A}^2),$
$\hspace{2mm}\rule[-1mm]{0mm}{7.5mm} \displaystyle Y_{i}\sim \mbox{N}(\mu_B, {\sigma_B}^2)$
とすれば
$\hspace{2mm}\rule[-1mm]{0mm}{7.5mm} \displaystyle \frac{\overline{X}-\overline{Y}-(\mu_A-\mu_B)}{\sqrt{\frac{{\sigma_A}^2}{5}+\frac{{\sigma_B}^2}{6}}}\sim \mbox{N}(0,1)$
である.帰無仮説$H_0$および${\sigma_A}^2={\sigma_B}^2$の仮定からプールされた分散$U^2$を用いて
$\hspace{2mm}\rule[-1mm]{0mm}{7.5mm} \displaystyle \frac{\overline{X}-\overline{Y}}{\sqrt{\frac{{U}^2}{5}+\frac{{U}^2}{6}}}\sim t(5+6-2)=t(9)$
となる.棄却域は$t>t_{0.05}(9)=1.833$.プールされた分散の実現値は$\hspace{2mm}\rule[-1mm]{0mm}{7.5mm} \displaystyle u^2=\frac{(5-1)\cdot182.8+(6-1)\cdot 211.5 }{5+6-2}$
$\hspace{8.5mm}\rule[-1mm]{0mm}{7.5mm} =198.7\cdots $
となるから,実現値は
$\hspace{2mm}\rule[-1mm]{0mm}{7.5mm} \displaystyle \frac{\overline{x}-\overline{y}}{\sqrt{\frac{{u}^2}{5}+\frac{{u}^2}{6}}}=\frac{54.4-41.7}{\sqrt{198.7(\frac15+\frac16)}}$
$\hspace{27mm}\rule[-1mm]{0mm}{7.5mm} \displaystyle =1.48\cdots <1.833$
よって$H_0$は棄却されない.すなわちA大学出身者の学生が成績が良いとは言えない.
問2
全国チェーンのハンバーガーショップの店舗A,Bが販売するハンバーガーについて,「店舗Aのハンバーガーは店舗Bのものよりも重量のばらつきが大きい」との指摘がある.そこで,店舗Aのハンバーガーの重量の分布の母分散が店舗Bのものよりも大きいか検証することとした.以下のデータをもとに,有意水準5%で検定せよ.ただし,ハンバーガーの重量(g)は正規分布に従うとせよ.
店舗A:見本数$21$,標本平均$105.0$, 不偏分散$4.5$
店舗B:見本数$16$,標本平均$106.5$, 不偏分散$2.5$
解答はこちら
解
店舗A,Bのハンバーガーの重量の分布をそれぞれ$\mbox{N}(\mu_A, {\sigma_A}^2), \mbox{N}(\mu_B, {\sigma_B}^2)$,不偏分散をそれぞれ${U_A}^2, {U_B}^2$とおく.店舗Aの方が分散が大きいかどうか検証したいのだから,
$\hspace{2mm}\rule[-1mm]{0mm}{7.5mm} \displaystyle H_0: {\sigma_A}^2={\sigma_B}^2$,$H_1:{\sigma_A}^2>{\sigma_B}^2$
とすればよい.$H_0$のもとで,
$\hspace{2mm}\rule[-1mm]{0mm}{7.5mm} \displaystyle F=\frac{{U_A}^2/{\sigma_A}^2}{{U_B}^2/{\sigma_B}^2}=\frac{{U_A}^2}{{U_B}^2}\sim F(20,15)$
棄却域は$f>F_{0.05}(20, 15)=2.328$.実現値を計算すると
$\hspace{2mm}\rule[-1mm]{0mm}{7.5mm} \displaystyle f=\frac{{u_A}^2}{{u_B}^2}=\frac{4.5}{2.5}=1.8<2.328$
となり,$H_0$は棄却されない.すなわち店舗Aのハンバーガーの重量がばらつきが大きいとは言えない.

本ブログ・解説動画に対応した資料です(note)
この記事の動画解説版はこちら↓









