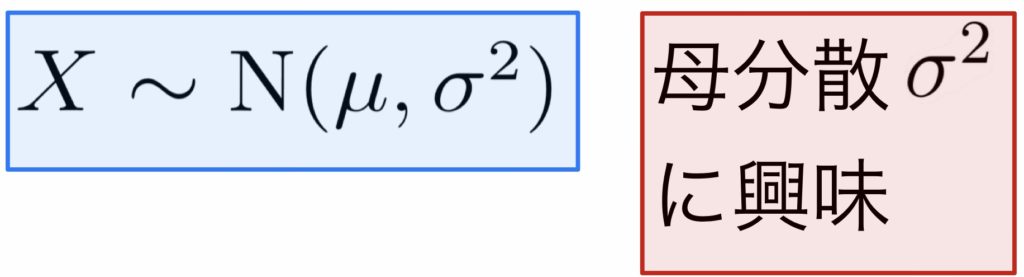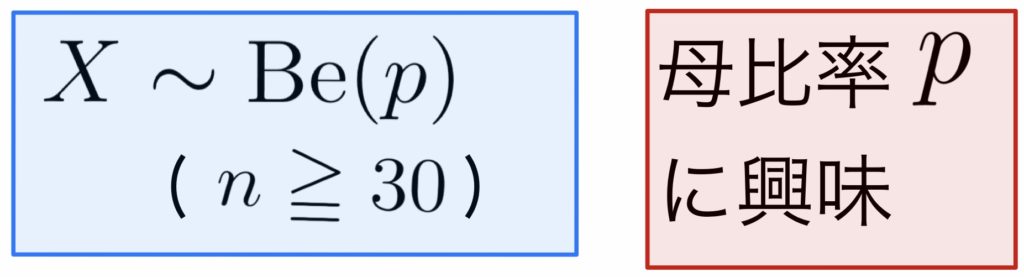この記事の動画解説版はこちら→統計チャンネル
よく使う仮説検定の手法(1標本)をまとめる．(検定)統計量の形は母集団分布と興味のある母数の組み合わせから計算できる．また，以下表では有意水準$\alpha$，右側検定とする(記事45でも同様)
母集団分布，興味のある母数，仮説
$H_0: \mu=\mu_0, \ H_1: \mu > \mu_0$
$\sigma^2$が既知のとき
\( \displaystyle \rule[-1mm]{0mm}{7.5mm}Z=\frac{\overline{X}-\mu0}{\sqrt{\sigma^2/n}}\sim \mbox{N}(0,1) \)
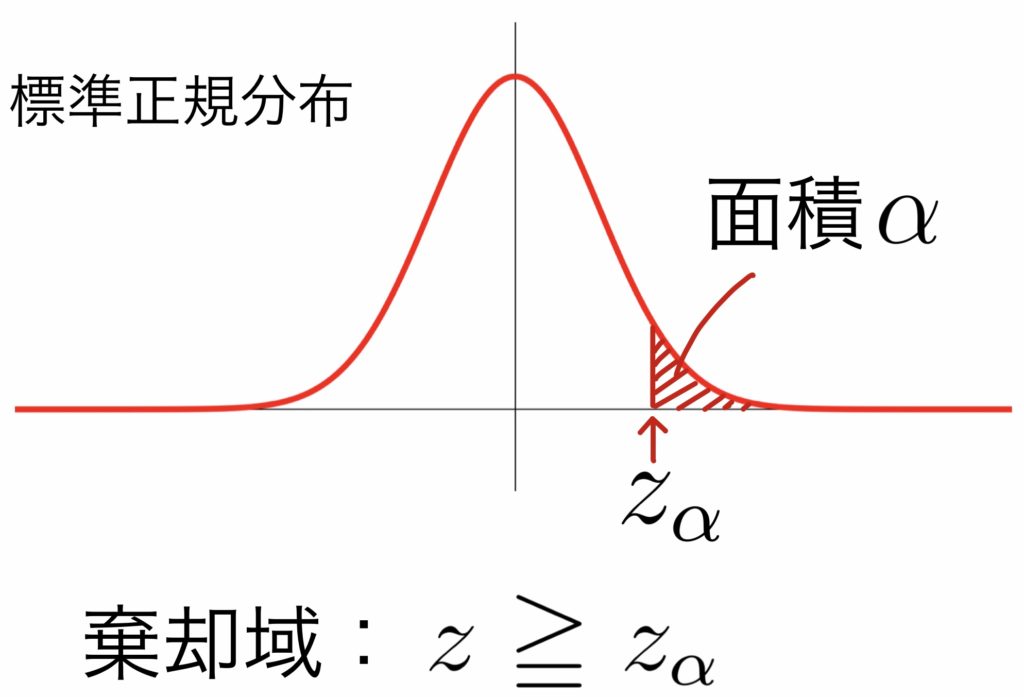
$\rule[-1mm]{0mm}{10.5mm}$棄却域は \( \displaystyle \rule[-1mm]{0mm}{7.5mm} z\geqq z_{\alpha}\)
$\sigma^2$が未知のとき
\( \displaystyle \rule[-1mm]{0mm}{7.5mm}T=\frac{\overline{X}-\mu_0}{\sqrt{U^2/n}}\sim t(n-1) \)
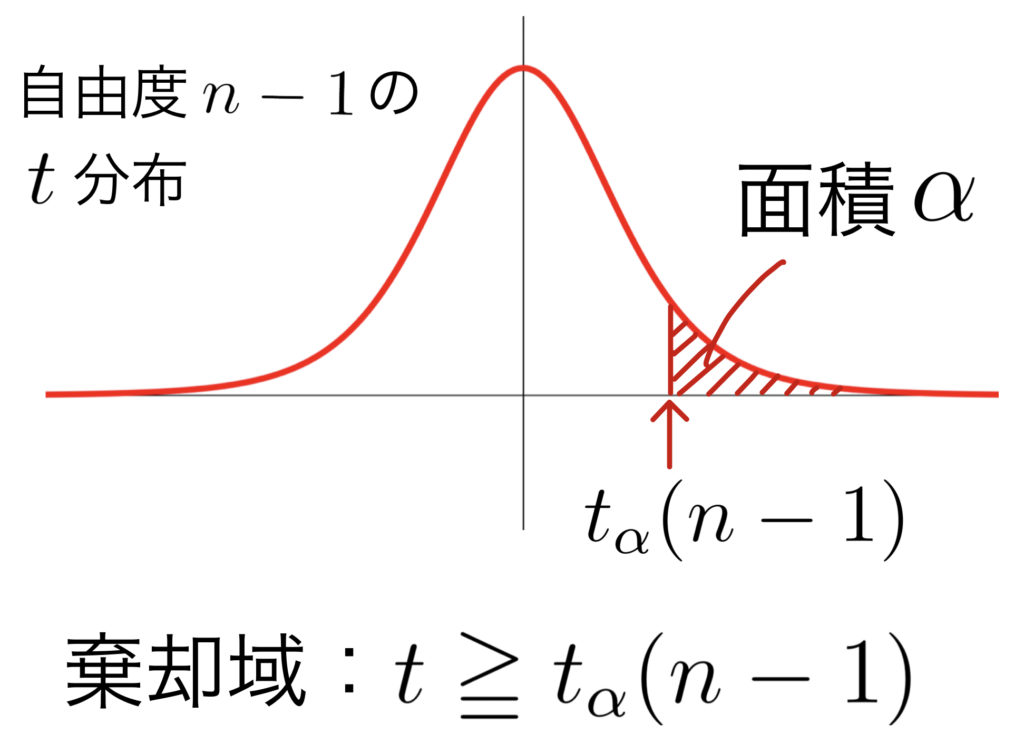
棄却域は \( \displaystyle \rule[-1mm]{0mm}{10.5mm} t\geqq t_{\alpha}(n-1)\)
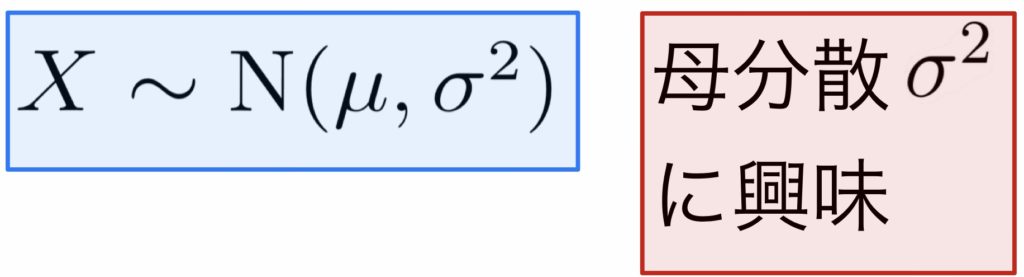
$H_0: \sigma^2={\sigma_0}^2, \ H_1: \sigma^2>{\sigma_0}^2$
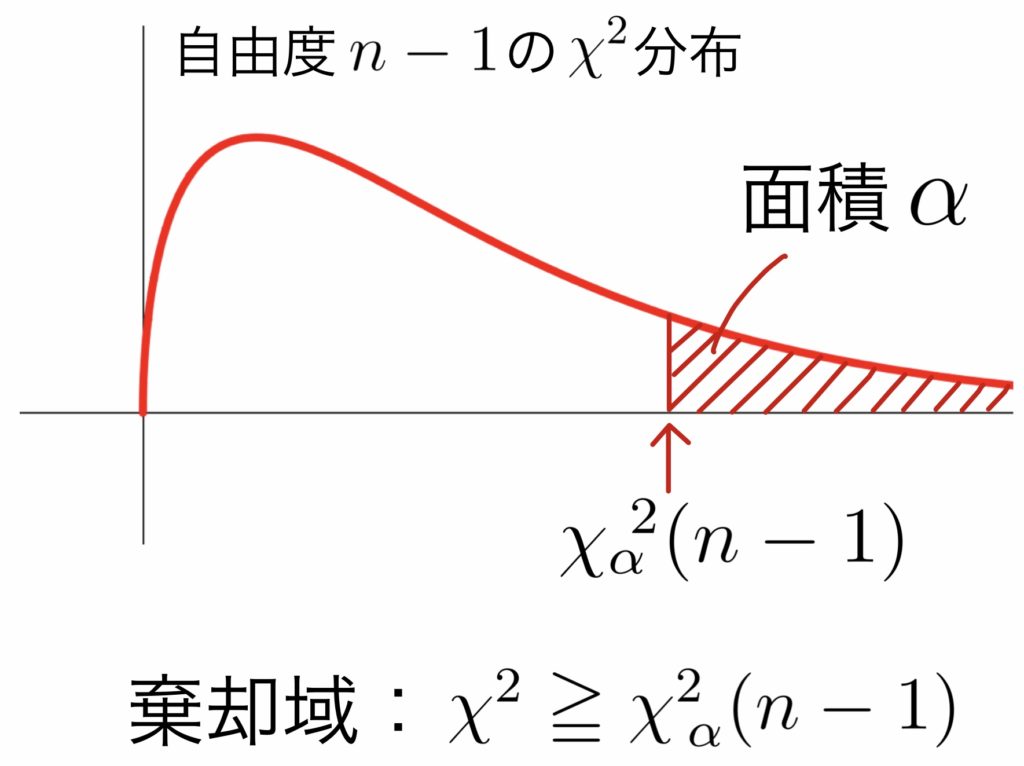
\( \displaystyle \rule[-1mm]{0mm}{7.5mm} \chi^2=\frac{(n-1)U^2}{{\sigma_0}^2}\sim \chi^2(n-1) \)
$\rule[-1mm]{0mm}{10.5mm}$ 棄却域は \( \displaystyle \rule[-1mm]{0mm}{7.5mm} \chi^2\geqq {\chi^2}_{\!\alpha}(n-1)\)
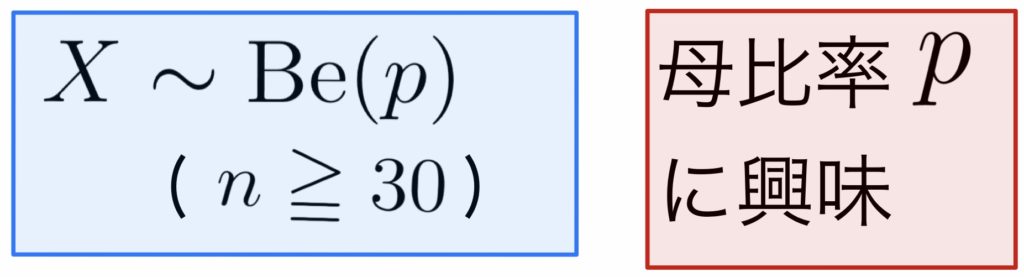
$H_0: p=p_0, \ H_1: p >p_0$
\( \displaystyle \rule[-1mm]{0mm}{7.5mm}Z=\frac{\hat{P}-p_0}{\sqrt{p_0(1-p_0)/n}}\sim\mbox{N}(0,1) \)
棄却域は $ \rule[-1mm]{0mm}{10.5mm} z\geqq z_{\alpha}$
$\rule[-1mm]{0mm}{10.5mm}$(例) ある牛丼屋では，標準サイズの牛丼に使用するご飯260gを機械Aを用いて盛り付けている．あるとき「盛り付けられるご飯の量が260gよりも多いのではないか」とする指摘があり，この機械Aが盛り付けるご飯20回分を無作為に選び，計測すると平均が262g，不偏分散が9.0gであった．機械Aが盛り付けるご飯の平均量は260gより多いと判断できるか，有意水準5%で検定せよ．ただし，機械Aが盛り付けるご飯の量は正規分布に従うと仮定してよい．
(解)
機械$A$が盛り付けるご飯の量を$X_i$とおくと，ある正規分布に従う($X_i\sim \mbox{N}(\mu, \sigma^2)$)．盛り付けるご飯の量が多いかどうかを検証したいのだから，
帰無仮説$H_0: \mu=260$，対立仮説$H_1: \mu>260$
とすればよい．
帰無仮説$H_0$のもとで，
$\hspace{5mm}\rule[-1mm]{0mm}{7.5mm} \displaystyle X_i\sim \mbox{N}(260, \sigma^2)$
すなわち
$\hspace{5mm}\rule[-1mm]{0mm}{7.5mm} \displaystyle \overline{X}=\frac{1}{20}\sum_{i=1}^{n}X_i\sim\mbox{N}\left(260, \frac{\sigma^2}{20}\right)$
標準化すれば
$\hspace{5mm}\rule[-1mm]{0mm}{7.5mm} \displaystyle \frac{\overline{X}-260}{\sqrt{\sigma^2/20}}\sim\mbox{N}(0,1^2)$
母分散は不明であるから$\sigma^2$は不偏分散$U^2$に取り替えて
$\hspace{5mm}\rule[-1mm]{0mm}{7.5mm} \displaystyle \frac{\overline{X}-260}{\sqrt{U^2/20}}\sim t(19)$
棄却域は$t > t_{0.05}(19)=1.729$．
実現値は
$\hspace{5mm}\rule[-1mm]{0mm}{7.5mm} \displaystyle \frac{\overline{x}-260}{\sqrt{u^2/20}}=\frac{262-260}{\sqrt{9.0/20}}=2.98\cdots >1.729$
よって$H_0$を棄却し，$H_1$を採択する．すなわち機械$A$が盛り付けるご飯の平均量は$260\mbox{g}$よりも多いと結論する．
正規分布 $\mbox{N}(5,\sigma^2)$ から大きさ6の標本を無作為抽出すると，次の表のようになった．母分散は $\sigma^2=2^2$ 程度とされていたが，やや大きいように感じるので，検定を行うことにした．帰無仮説 $H_0 : \sigma^2=2^2$ ，対立仮説 $H_1 : \sigma^2>2^2$ として有意水準 $5\%$ で検定をせよ．
あるサイコロを $600$ 回投げたら $1$ の目が $120$ 回出た．このサイコロは通常のサイコロと比べて $1$ の目が出やすいと言えるか，有意水準 $5\%$ で検定せよ．
本ブログ・解説動画に対応した資料です(note)
この記事の動画解説版はこちら↓
| 前の記事へ戻る 43 仮説検定の一般的な手順 |
次の記事へ 45 よく使う仮説検定一覧(2標本)その1 |
| 記事一覧へ戻る 統計学の基礎シリーズ 目次 |
|